题目内容
2.解下列方程组:(1)$\left\{\begin{array}{l}{x=3y-5}\\{3y=8-2x}\end{array}\right.$
(2)$\left\{\begin{array}{l}{2x-y=3}\\{5x-3(x+y)=7}\end{array}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x=3y-5①}\\{3y=8-2x②}\end{array}\right.$,
把①代入②得:3y=8-6y+10,
解得:y=2,
把y=2代入①得:x=1,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{2x-y=3①}\\{2x-3y=7②}\end{array}\right.$,
①-②得:2y=-4,
解得:y=-2,
把y=-2代入①得:x=$\frac{1}{2}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=-2}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
10.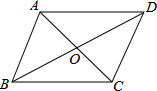 如图,要使平行四边形ABCD是矩形,可添加的条件是( )
如图,要使平行四边形ABCD是矩形,可添加的条件是( )
 如图,要使平行四边形ABCD是矩形,可添加的条件是( )
如图,要使平行四边形ABCD是矩形,可添加的条件是( )| A. | OA=OC OB=OD | B. | AC=BD | C. | AB=BC | D. | AC⊥BD |
 在正方形网格中,每个小正方形的边长为1个单位长度,三角形ABC的三个顶点位置如图所示,平移三角形ABC,使点A移动到点A′.
在正方形网格中,每个小正方形的边长为1个单位长度,三角形ABC的三个顶点位置如图所示,平移三角形ABC,使点A移动到点A′. 如图,△ABC中,AB=AC=10,AD⊥BC于D,AD=8,求S△ABC.
如图,△ABC中,AB=AC=10,AD⊥BC于D,AD=8,求S△ABC.
 在平面直角坐标系xOy中,抛物线y=ax2-4ax+4a-3(a≠0)的顶点为A.
在平面直角坐标系xOy中,抛物线y=ax2-4ax+4a-3(a≠0)的顶点为A.