题目内容
7.先化简,再求值:$({\frac{3x+4}{{{x^2}-1}}-\frac{2}{x-1}})÷\frac{x+2}{{{x^2}-2x+1}}$,其中x是不等式组$\left\{\begin{array}{l}x+4>0\\ 2x+6<1\end{array}$的整数解.分析 先根据分式混合运算的法则把原式进行化简,求出x的值代入进行计算即可.
解答 解:原式=$\frac{3x+4-2(x+1)}{(x+1)(x-1)}$÷$\frac{x+2}{{x}^{2}-2x+1}$
=$\frac{x+2}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{x+2}$
=$\frac{x-1}{x+1}$,
解不等式组$\left\{\begin{array}{l}x+4>0\\ 2x+6<1\end{array}\right.$得,-4<x<-$\frac{5}{2}$,
∵x是不等式组的整数解,
∴x=-3,
∴原式=$\frac{-3-1}{-3+1}$=2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
15.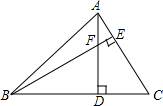 如图,在△ABC中,∠ABC=45°,AC=5,F是高AD和BE的交点,则BF的长是( )
如图,在△ABC中,∠ABC=45°,AC=5,F是高AD和BE的交点,则BF的长是( )
 如图,在△ABC中,∠ABC=45°,AC=5,F是高AD和BE的交点,则BF的长是( )
如图,在△ABC中,∠ABC=45°,AC=5,F是高AD和BE的交点,则BF的长是( )| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
12.描点法是研究函数图象的重要方法.那么对函数y=-x-$\frac{1}{x}$,你如果采用描点法的话,能得到该函数的正确性质是( )
| A. | 该函数图象与x轴相交 | B. | 该函数图象与y轴相交 | ||
| C. | 该函数图象关于原点成中心对称 | D. | 该函数图象是轴对称图形 |
16.使代数式$\frac{3}{2x-3}$有意义的x的取值范围是( )
| A. | x<$\frac{3}{2}$ | B. | x=$\frac{3}{2}$ | C. | x>$\frac{3}{2}$ | D. | x≠$\frac{3}{2}$ |
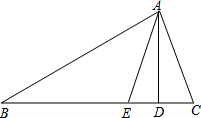 如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=30°,∠DAE=20°,
如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=30°,∠DAE=20°,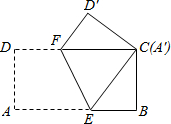 如图,将长为12cm,宽6cm的矩形纸片ABCD折叠,使点A与点C重合,则折痕EF的长为3$\sqrt{5}$cm.
如图,将长为12cm,宽6cm的矩形纸片ABCD折叠,使点A与点C重合,则折痕EF的长为3$\sqrt{5}$cm.