题目内容
15.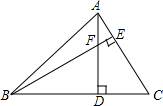 如图,在△ABC中,∠ABC=45°,AC=5,F是高AD和BE的交点,则BF的长是( )
如图,在△ABC中,∠ABC=45°,AC=5,F是高AD和BE的交点,则BF的长是( )| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
分析 求出∠ADC=∠BDF,∠DBF=∠DAC,AD=BD,根据ASA推出△ADC≌△BDF,根据全等三角形的性质推出AC=BF即可.
解答 解:∵AD、BE是高,
∴∠ADC=∠BDF=90°,∠BEC=90°,
∴∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
∵∠ABC=45°,∠ADB=90°,
∴∠BAD=∠ABD=45°,
∴AD=BD,
在△ADC和△BDF中
$\left\{\begin{array}{l}{∠ADC=∠BDF}\\{AD=BD}\\{∠DAC=∠DBF}\end{array}\right.$
∴△ADC≌△BDF(ASA),
∴BF=AC,
∵AC=5,
∴BF=5,
故选C.
点评 本题考查了三角形的内角和定理,等腰三角形的判定,全等三角形的性质和判定的应用,解此题的关键是推出△ADC≌△BDF,注意:全等三角形的对应边相等,难度适中.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
3.下列运算正确的是( )
| A. | a10+a5=a2 | B. | (a3)4=a7 | C. | (x-y)2=x2-y2 | D. | x3•(-x3)=-x6 |
20.下列计算正确的是( )
| A. | x•x3=x6 | B. | a2+a3=a5 | C. | (a3)2=a5 | D. | a3÷a=a2(a≠0) |
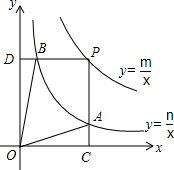 函数y=$\frac{m}{x}$和y=$\frac{n}{x}$在第一象限内的图象如图,点P是y=$\frac{m}{x}$的图象上一点,PC⊥x轴于点C,交y=$\frac{n}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{n}{x}$的图象于点B,且PA=3CA,tan∠DOB=$\frac{1}{5}$,SOAPB=3,则点B的坐标为($\frac{\sqrt{5}}{5}$,$\sqrt{5}$).
函数y=$\frac{m}{x}$和y=$\frac{n}{x}$在第一象限内的图象如图,点P是y=$\frac{m}{x}$的图象上一点,PC⊥x轴于点C,交y=$\frac{n}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{n}{x}$的图象于点B,且PA=3CA,tan∠DOB=$\frac{1}{5}$,SOAPB=3,则点B的坐标为($\frac{\sqrt{5}}{5}$,$\sqrt{5}$).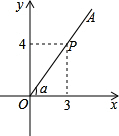 如图,P是∠α的边OA上一点,且P点的坐标为(3,4),则sin(90°-α)=$\frac{3}{5}$.
如图,P是∠α的边OA上一点,且P点的坐标为(3,4),则sin(90°-α)=$\frac{3}{5}$.