Question

16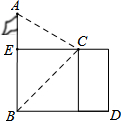．如图，某人站在楼顶观测对面的笔直的旗杆AB，已知观测点C到旗杆的距离CE=8m，测得旗杆的顶部A的仰角∠ECA=30°，旗杆底部B的俯角∠ECB=45°，那么旗杆AB的高度是（　　）

• A． （8$\sqrt{2}$+8$\sqrt{3}$）m
• B． （8+8$\sqrt{3}$）m
• C． （8$\sqrt{2}$+$\frac{8\sqrt{3}}{3}$）m
• D． （8+$\frac{8\sqrt{3}}{3}$）m

Answer 1

分析 在△AEC中利用∠ECA的正切值可求得AE；在△EBC中利用∠ECB的正切值可求得BE，根据AB=AE+BE即可求解．

解答 解：在△EBC中，有BE=EC×tan45°=8，
在Rt△AEC中，有AE=EC×tan30°=8×$\frac{\sqrt{3}}{3}$=$\frac{8\sqrt{3}}{3}$，
则AB=AE+BE=8+$\frac{8\sqrt{3}}{3}$（米）．
故选D．

点评 本题考查了解直角三角形的应用-仰角俯角问题，要求学生能借助其关系构造直角三角形并解直角三角形．