题目内容
9.已知直线y=$\frac{1}{2}$x+2与y轴交于点A,与双曲线y=$\frac{6}{x}$有一个交点为B(2,3),将直线AB向下平移,与x轴、y轴分别交于点C,D,与双曲线的一个交点为P,若$\frac{CD}{DP}$=$\frac{1}{2}$,则点D的坐标为(0,$\frac{\sqrt{2}}{2}$)或(0,-$\frac{\sqrt{2}}{2}$)或(0,$\frac{\sqrt{6}}{2}$)或(0,-$\frac{\sqrt{6}}{2}$),.分析 设D的坐标为(0,m),根据平行线分线段成比例定理得出$\frac{OD}{PM}$=$\frac{CD}{CP}$,然后根据$\frac{CD}{DP}$=$\frac{1}{2}$,求得PM的值,从而求得P的坐标,代入直线解析式即可求得m的值.
解答 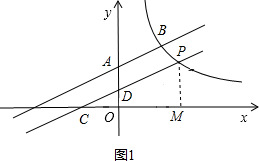 解;当D点在y轴的正半轴时,如图1所示,
解;当D点在y轴的正半轴时,如图1所示,
设D的坐标为(0,m),
∵将直线AB向下平移,与x轴、y轴分别交于点C,D,
∴CD∥AB,
∴直线CD的解析式为y=$\frac{1}{2}x$+m,
作PM⊥x轴于M,
∴PM∥y轴,
①P在第一象限时,$\frac{OD}{PM}$=$\frac{CD}{CP}$,
∵$\frac{CD}{DP}$=$\frac{1}{2}$,
∴$\frac{OD}{PM}$=$\frac{CD}{CP}$=$\frac{1}{3}$,
∴PM=3OD=3m,
∵P是双曲线的一个交点,
∴P($\frac{2}{m}$,3m),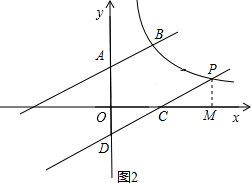
∴3m=$\frac{1}{2}$×$\frac{2}{m}$+m,
解得m=±$\frac{\sqrt{2}}{2}$,
∴m>0,
∴D(0,$\frac{\sqrt{2}}{2}$);
②P在第三象限时,$\frac{OD}{PM}$=$\frac{CD}{CP}$,
∵$\frac{CD}{DP}$=$\frac{1}{2}$,
∴$\frac{OD}{PM}$=$\frac{CD}{CP}$=1,
∴PM=OD=m,
∵P是双曲线的一个交点,
∴P(-$\frac{6}{m}$,-m),
∴-m=$\frac{1}{2}$×(-$\frac{6}{m}$)+m,
解得m=±$\frac{\sqrt{6}}{2}$,
∴m>0,
∴D(0,$\frac{\sqrt{6}}{2}$);
当D点在y轴的负半轴时,如图2所示,
作PM⊥x轴于M,
∴PM∥y轴,
③P在第一象限时,$\frac{OD}{PM}$=$\frac{CD}{CP}$,
∵$\frac{CD}{DP}$=$\frac{1}{2}$,
∴$\frac{OD}{PM}$=$\frac{CD}{CP}$=1,
∴PM=OD=m,
∵P是双曲线的一个交点,
∴P(-$\frac{6}{m}$,-m),
∴-m=$\frac{1}{2}$×(-$\frac{6}{m}$)+m,
解得m=±$\frac{\sqrt{6}}{2}$,
∴m<0,
∴D(0,-$\frac{\sqrt{6}}{2}$);
④P在第三象限时,$\frac{OD}{PM}$=$\frac{CD}{CP}$,
∵$\frac{CD}{DP}$=$\frac{1}{2}$,
∴$\frac{OD}{PM}$=$\frac{CD}{CP}$=$\frac{1}{3}$,
∴PM=3OD=3m,
∵P是双曲线的一个交点,
∴P(-$\frac{2}{m}$,-3m),
∴-3m=$\frac{1}{2}$×(-$\frac{2}{m}$)+m,
解得m=±$\frac{\sqrt{2}}{2}$,
∴m<0,
∴D(0,-$\frac{\sqrt{2}}{2}$);
综上,点D的坐标为(0,$\frac{\sqrt{2}}{2}$)或(0,-$\frac{\sqrt{2}}{2}$)或(0,$\frac{\sqrt{6}}{2}$)或(0,-$\frac{\sqrt{6}}{2}$),
故答案为(0,$\frac{\sqrt{2}}{2}$)或(0,-$\frac{\sqrt{2}}{2}$)或(0,$\frac{\sqrt{6}}{2}$)或(0,-$\frac{\sqrt{6}}{2}$).
点评 本题考查了反比例函数和一次函数的交点问题,平移的性质以及平行线分线段成比例定理,表示出P点的坐标是解题的关键.

| A. | 150元 | B. | 200元 | C. | 300元 | D. | 440元 |
| A. | 方程x2-4x+3=0是3倍根方程 | |
| B. | 若关于x的方程(x-3)(mx+n)=0是3倍根方程,则m+n=0 | |
| C. | 若m+n=0且m≠0,则关于x的方程(x-3)(mx+n)=0是3倍根方程 | |
| D. | 若3m+n=0且m≠0,则关于x的方程x2+(m-n)x-mn=0是3倍根方程 |
| A. | 1 | B. | -1 | C. | 2016 | D. | -2016 |
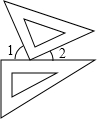 一副三角板按如图方式摆放,且∠1的度数比∠2的度数大54°,则∠1=( )
一副三角板按如图方式摆放,且∠1的度数比∠2的度数大54°,则∠1=( )| A. | 72° | B. | 70° | C. | 54° | D. | 18° |
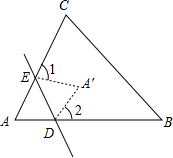 如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=68°,则∠1+∠2=136°.
如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=68°,则∠1+∠2=136°.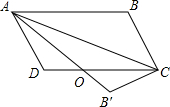 如图,在平行四边形ABCD中将△ABC沿AC对折,使点B落在B′处,AB′和CD相交于O,求证:OD=OB′.
如图,在平行四边形ABCD中将△ABC沿AC对折,使点B落在B′处,AB′和CD相交于O,求证:OD=OB′.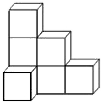 如图所示的几何体是由7个小正方体组合而成的立体图形,则它的俯视图是( )
如图所示的几何体是由7个小正方体组合而成的立体图形,则它的俯视图是( )