题目内容
19．
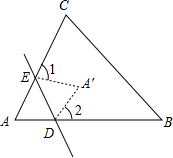如图，在折纸活动中，小明制作了一张△ABC纸片，点D、E分别是边AB、AC上，将△ABC沿着DE折叠压平，A与A′重合，若∠A=68°，则∠1+∠2=136°．
分析 根据三角形的内角和等于180°求出∠ADE+∠AED，再根据翻折变换的性质可得∠A′DE=∠ADE，∠A′ED=∠AED，然后利用平角等于180°列式计算即可得解．
解答 解：∵∠A=68°，
∴∠ADE+∠AED=180°-68°=112°，
∵△ABC沿着DE折叠压平，A与A′重合，
∴∠A′DE=∠ADE，∠A′ED=∠AED，
∴∠1+∠2=180°-（∠A′ED+∠AED）+180°-（∠A′DE+∠ADE）=360°-2×112°=136°．
故答案为：136．
点评 本题考查了三角形的内角和定理，翻折变换的性质，整体思想的利用求解更简便．
练习册系列答案
相关题目
10．用科学记数法表示31410000（ ）
| A． | 3.14×107 | B． | 3.141×107 | C． | 3.141×108 | D． | 3.141×106 |
7．（-2xy）4的计算结果是（ ）
| A． | -2x4y4 | B． | 8x4y4 | C． | 16xy4 | D． | 16x4y4 |
4．甲校男生占全校总人数的50%，乙校女生占全校总人数的50%，则甲乙两校女生人数相比（ ）
| A． | 甲校多于乙校 | B． | 甲校少于乙校 | C． | 甲乙两校一样多 | D． | 不能确定 |
如图，直线a∥b，c∥d，∠1=115°，则∠3=65°．
8．在“等边三角形、正方形、等腰梯形、平行四边形、矩形、正六边形”中，任取其中一个圆形，恰好是中心对称图形的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |