��Ŀ����
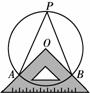
�����龳����ͼ1��ֱ�����ǰ�ABC�У���C��90�㣬AC��BC����һ�����㹻���ĵ�ϸ��˿������ֱ�ǵĶ���D����ֱ�����ǰ�ABC��б��AB�ϣ��ٽ���ֱ���Ƶ�D��ת����ʹ�����߷ֱ������ǰ��AC�ߡ�BC�߽���P��Q���㡣
����̽������1������ת�����У�
����ͼ2����AD��BDʱ���߶�DP��DQ�к�������ϵ����˵�����ɡ�
����ͼ3����AD��2BDʱ���߶�DP��DQ�к�������ϵ����˵�����ɡ�
�۸�����Ԣ١��ڵ�̽���������д����AD��nBDʱ��DP��DQ�����������ϵΪ_______________��ֱ��д�����ۣ�����֤����
��2����AD��BDʱ����AB��20������PQ�����DPQ�����ΪS������ת�����У�S�Ƿ������Сֵ�����ֵ�������ڣ������Сֵ�����ֵ���������ڣ���˵�����ɡ�

ͼ1 ͼ2 ͼ3
��1����DP��DQ
���ɣ�����CD��
 ����ABC�ǵ���ֱ�������Σ�
����ABC�ǵ���ֱ�������Σ�
 ����A����DCQ����ADC��90�㣬���ADP����PDC����CDQ����PDC��90�㣬
����A����DCQ����ADC��90�㣬���ADP����PDC����CDQ����PDC��90�㣬
���ADP����CDQ�����ADP�ա�CDQ��
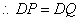
��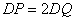 ��
��
���ɣ���ͼ������D��DM��AC��DN��BC������ֱ�ΪM��N��

���DMP����DNQ��90�㣬���MDP����NDQ��
���DPM�ס�DQN�� ��
��
�ߡ�AMD����DNB��90�㣬��A����B��
���AMD�ס�BND��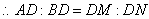 ��
��
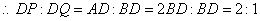 ��
��
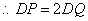 ��
��
��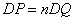 ��
��
��2�����ڣ��� ���ɣ�1����֪
���ɣ�1����֪ ��
��

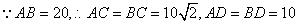 ��
��
��DP��ACʱ��x��С����Сֵ��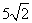 ����ʱ��S����Сֵ��
����ʱ��S����Сֵ��
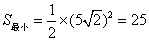
����P���A�غ�ʱ��x������ֵ��10����ʱ��S�����ֵ��

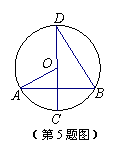
 ����D��0��3
����D��0��3 ��������l����D����x��ƽ�У���P��Q�ֱ���l��x���������϶��㣬�����PQO=60�㣮
��������l����D����x��ƽ�У���P��Q�ֱ���l��x���������϶��㣬�����PQO=60�㣮
 S��x�ĺ�����ϵʽ����Ӧ���Ա�
S��x�ĺ�����ϵʽ����Ӧ���Ա�