��Ŀ����
��ͼ������OABC�У�A��6��0����C��0��2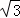 ����D��0��3
����D��0��3 ��������l����D����x��ƽ�У���P��Q�ֱ���l��x���������϶��㣬�����PQO=60�㣮
��������l����D����x��ƽ�У���P��Q�ֱ���l��x���������϶��㣬�����PQO=60�㣮
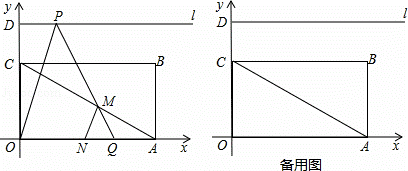
��1���ٵ�B�������������ڡ�CAO=�� �ȣ��۵���Q���A�غ�ʱ����P������Ϊ �� ����ֱ��д���𰸣�
��2����OA���е�ΪN��PQ���߶�AC�ཻ�ڵ�M���Ƿ���ڵ�P��ʹ��AMNΪ���������Σ������ڣ���ֱ��д����P�ĺ�����Ϊm���������ڣ���˵�����ɣ�
��3�����P�ĺ�����Ϊx����OPQ�����OABC���ص����ֵ����ΪS������ S��x�ĺ�����ϵʽ����Ӧ���Ա�
S��x�ĺ�����ϵʽ����Ӧ���Ա� ��x��ȡֵ��Χ��
��x��ȡֵ��Χ��
�⣺��1���٣�6��2 ���� ��30���ۣ�3��3
���� ��30���ۣ�3��3 ����
����
 ��2�����ڡ�m=0��m=3﹣
��2�����ڡ�m=0��m=3﹣ ��m=2�� ��3����0��x��3ʱ��
��m=2�� ��3����0��x��3ʱ��
��ͼ1��OI=x��IQ=PI•tan60��=3��O Q=OI+IQ=3+x��
Q=OI+IQ=3+x��
�������ֱ֪��l��BC��OA��
�ɵ� ����EF=
����EF= ��3+x����
��3+x����
��ʱ�ص����������Σ������Ϊ��

 ��3��x��5ʱ����ͼ2��
��3��x��5ʱ����ͼ2��

��5��x��9ʱ����ͼ3��


��x��9ʱ����ͼ4��
 ��
��
����������S��x�ĺ�����ϵʽΪ��

 ��
��

 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д� ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д���ͼ����������ABCD�У��Խ���BD�ij�Ϊ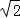 ������BD�Ƶ�B��ת��D����BC�ӳ����ϵĵ�D�䴦����D������·��Ϊ
������BD�Ƶ�B��ת��D����BC�ӳ����ϵĵ�D�䴦����D������·��Ϊ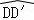 ����ͼ����Ӱ���ֵ�����ǣ�������
����ͼ����Ӱ���ֵ�����ǣ�������

| �� | A�� |
| B�� |
| C�� |
| D�� | ��2 |
 ��1
��1
 ��
��
 ������,��
������,�� ,��������Բ����,��
,��������Բ����,�� �� .
�� .
 �飩��ʽ���ǣ� ��
�飩��ʽ���ǣ� ��  ���� B���������¿��ŵ��˼ҼҾ�ÿ��������ĵ���
���� B���������¿��ŵ��˼ҼҾ�ÿ��������ĵ��� ��x��0����
��x��0����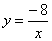 ��x��0����ͼ��
��x��0����ͼ��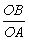 ��ֵΪ��������
��ֵΪ��������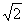 B��2 C��
B��2 C��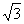 D��3
D��3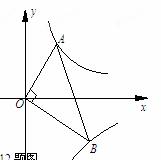
 ���Ա���
���Ա��� ��ȡֵ��Χ�ǣ� ����
��ȡֵ��Χ�ǣ� ���� B��
B�� C��
C�� D��
D��