题目内容
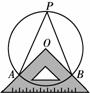
如图,将三角板的直角顶点放在⊙O的圆心上,两条直角边分别交⊙O于A、B两点,点P在优弧AB上,且与点A、B不重合,连结PA、PB.则∠APB的大小为 度.
 |
(
45

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
题目内容
如图,将三角板的直角顶点放在⊙O的圆心上,两条直角边分别交⊙O于A、B两点,点P在优弧AB上,且与点A、B不重合,连结PA、PB.则∠APB的大小为 度.
 |
(
45

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案