题目内容
19.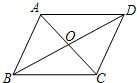 如图,四边形ABCD的对角线AC,BD交于O点,且AB$\stackrel{∥}{=}$CD,那么图中的全等三角形有( )
如图,四边形ABCD的对角线AC,BD交于O点,且AB$\stackrel{∥}{=}$CD,那么图中的全等三角形有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
分析 首先根据一组对边平行且相等的四边形是平行四边形可得四边形ABCD是平行四边形,可得AO=CO,BO=DO,再证明△AOB≌△COD,同理可得△AOD≌△COB,然后再证明△ABD≌△CDB同理可得△ABC≌△CDA.
解答 解:∵四边形ABCD中AB$\stackrel{∥}{=}$CD,
∴四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
在△AOB和△COD中$\left\{\begin{array}{l}{AO=CO}\\{∠AOB=∠COD}\\{BO=DO}\end{array}\right.$,
∴△AOB≌△COD(SAS),
同理可得△AOD≌△COB,
∴AD=BC,
在△ABD和△CDB中$\left\{\begin{array}{l}{AD=BC}\\{AB=CD}\\{BD=BD}\end{array}\right.$,
∴△ABD≌△CDB(SSS),
同理可得△ABC≌△CDA,
共4对,
故选:C.
点评 此题主要考查了全等三角形的判定,以及平行四边形的判定和性质,关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图是一个正方体纸盒的展开图,当折成纸盒时,与点1重合的点是7和11.
如图是一个正方体纸盒的展开图,当折成纸盒时,与点1重合的点是7和11.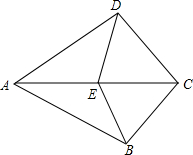 已知:∠ABC=∠ADC=90°,E是AC中点.
已知:∠ABC=∠ADC=90°,E是AC中点. 如图,已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连结AE、AF、EF.
如图,已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连结AE、AF、EF. ∠AOB的大小可由量角器测得(如图所示),则∠AOB的补角的大小为120°.
∠AOB的大小可由量角器测得(如图所示),则∠AOB的补角的大小为120°. 在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(-1,a),B(3,a),且最低点的纵坐标为-4.
在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(-1,a),B(3,a),且最低点的纵坐标为-4. 如图,将△ABC纸片折叠,使点A落在边BC上,记落点为点D,且折痕EF∥BC,若EF=3,则BC的长度为6.
如图,将△ABC纸片折叠,使点A落在边BC上,记落点为点D,且折痕EF∥BC,若EF=3,则BC的长度为6.