题目内容
19.已知平面直角坐标系中有点A(-2,1),B(2,3)(1)在x轴上找一点P,使|PA-PB|的值最大,并求出点P的坐标;
(2)在x轴上找一点M,使MA+MB的值最小,并求出点M的坐标;
(3)在x轴上找一点N,使△ABN为等腰三角形,通过画图说明使△ABN为等腰三角形的点N有多少个(不求N点坐标).
分析 (1)根据两边之差小于第三边得到P位于直线AB与x轴交点的位置时,|PA-PB|最大,设直线AB解析式为y=kx+b,将A与B坐标代入,求出k与b的值,确定出直线AB解析式,令y=0求出对应x的值,确定出P的坐标;
(2)利用轴对称图形的性质可作点A关于x轴的对称点A′,连接A′B,交x轴于点M,点M即为所求.根据A(-2,1),B(2,3)两点的坐标用待定系数法求出直线A′B的解析式,再根据x轴上的点的坐标特征求出点M的坐标.
(3)以点A为圆心,AB长为半径交x轴于两点;以点B为圆心,AB长为半径交x轴于两点;AB的垂直平分线交x轴于一点,点N共5个.
解答  解:(1)解:设直线AB的解析式为y=kx+b(k≠0),
解:(1)解:设直线AB的解析式为y=kx+b(k≠0),
将A(-2,1),B(2,3)代入得:$\left\{\begin{array}{l}{-2k+b=1}\\{2k+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=2}\end{array}\right.$,
故直线AB解析式为y=-$\frac{1}{2}$x+2,
令y=0,解得x=4,
即P坐标为(4,0)时,|PA-PB|最大;
(2)点A关于x轴的对称点A′(-2,-1),
直线A′B的解析式为y=x+1.
点M为直线A′B与x轴的交点,
∴点M的坐标为(-1,0).
(3)如图所示:使△ABN为等腰三角形的点N有5个.
点评 此题主要考查轴对称--最短路线问题,综合运用了一次函数的知识.同时考查了等腰三角形的作图方法.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
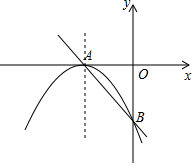 如图,直线y=-x-2交x轴于点A,交y轴于点B,抛物线y=a(x-h)2的顶点为A,且经过点B.
如图,直线y=-x-2交x轴于点A,交y轴于点B,抛物线y=a(x-h)2的顶点为A,且经过点B.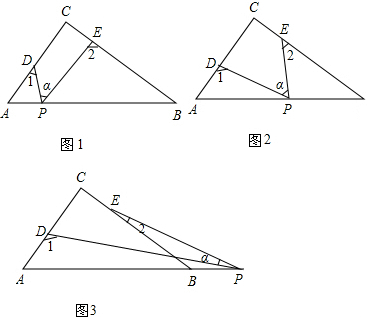
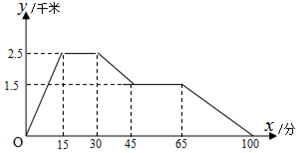 下面的图象反映的过程是:李华从家跑步去体育场,在那里锻炼了一阵后又走到书店去买书,然后散步走回家.其中x表示时间,y表示李华离家的距离.
下面的图象反映的过程是:李华从家跑步去体育场,在那里锻炼了一阵后又走到书店去买书,然后散步走回家.其中x表示时间,y表示李华离家的距离.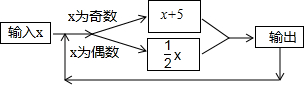 如图所示的运算程序中,若开始输入的x值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,…第2012次输出的结果为1.
如图所示的运算程序中,若开始输入的x值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,…第2012次输出的结果为1. 某工厂加工一种包装盒,如图所示是包装盒的表面展开图.
某工厂加工一种包装盒,如图所示是包装盒的表面展开图.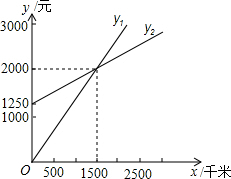 李明准备租用一辆出租车搞个体营运,现有甲乙两家出租车公司可以和他签订合同,设汽车每月行驶x千米,应付给甲公司的月租费y1元,应付给乙公司的月租费是y2元,y1、y2与x之间的函数关系的图象如图所示,请根据图象回答下列问题:
李明准备租用一辆出租车搞个体营运,现有甲乙两家出租车公司可以和他签订合同,设汽车每月行驶x千米,应付给甲公司的月租费y1元,应付给乙公司的月租费是y2元,y1、y2与x之间的函数关系的图象如图所示,请根据图象回答下列问题: