题目内容
18.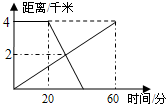 已知A,B两地相距4千米,上午8:00时,甲从A地步行到B地,8:20时乙从B地出发骑自行车到A地,甲、乙两人离A地的距离y(千米)与甲所用的时间x(分)之间的关系如图所示,则下列说法错误的是 ( )
已知A,B两地相距4千米,上午8:00时,甲从A地步行到B地,8:20时乙从B地出发骑自行车到A地,甲、乙两人离A地的距离y(千米)与甲所用的时间x(分)之间的关系如图所示,则下列说法错误的是 ( )| A. | 两人于8:30在途中相遇 | B. | 乙8:45到达A地 | ||
| C. | 甲步行的速度是4千米/时 | D. | 乙骑车的速度是$\frac{1}{5}$千米/分 |
分析 根据甲60分走完全程4千米,求出甲的速度,再由图中两图象的交点可知,两人在走了2千米时相遇,从而可求出甲此时用了0.5小时,则乙用了(0.5-$\frac{1}{3}$)小时,所以乙的速度为:2÷$\frac{1}{6}$,求出乙走完全程需要时间,此时的时间应加上乙先前迟出发的20分,即可求出答案.
解答 解:因为甲60分走完全程4千米,所以甲的速度是4千米/时,
由图中看出两人在走了2千米时相遇,那么甲此时用了0.5小时,则乙用了(0.5-$\frac{1}{3}$)小时=$\frac{1}{6}$小时,
∴乙的速度为:2÷$\frac{1}{6}$=12千米|小时=$\frac{1}{5}$千米|分,
∴甲到遇点用是8:30,即两人于8:30在途中相遇,
∴乙走完全程需要时间为:4÷12=$\frac{1}{3}$(时)=20分,此时的时间应加上乙先前迟出发的20分,现在的时间为8点40,
故A正确,C正确,B错误,D正确,
故选B.
点评 本题主要考查了函数图象的应用.做题过程中应根据实际情况和具体数据进行分析.本题应注意乙用的时间和具体时间之间的关联.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
8. 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )
 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
9.代数式$\sqrt{6-x}$有意义时,实数x的取值范围是( )
| A. | x>6 | B. | x≤6 | C. | x<6 | D. | x≠6 |
6.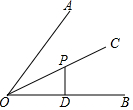 如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
 如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 4 |
13.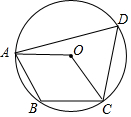 如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠DAO+∠DCO的大小为( )
如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠DAO+∠DCO的大小为( )
 如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠DAO+∠DCO的大小为( )
如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠DAO+∠DCO的大小为( )| A. | 45° | B. | 50° | C. | 60° | D. | 75° |
10.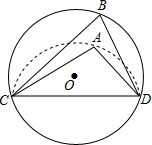 如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=110°,则∠B的度数是( )
如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=110°,则∠B的度数是( )
 如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=110°,则∠B的度数是( )
如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=110°,则∠B的度数是( )| A. | 110° | B. | 70° | C. | 60° | D. | 55° |
 如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为5.
如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为5.