题目内容

10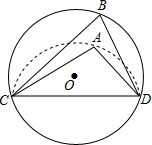．如图，CD是⊙O的弦，O是圆心，把⊙O的劣弧沿着CD对折，A是对折后劣弧上的一点，∠CAD=110°，则∠B的度数是（　　）
A．110°B．70°C．60°D．55°

分析 由已知条件先求出∠A'=100，再利用圆内接四边形的性质即可求出∠B的度数．

解答 解：如图，翻折△ACD，点A落在A'处，

∴∠A'=∠A=110°，
∵四边形A'CBD是⊙O的内接四边形，
∴∠A'+∠B=180°，
∴∠B=70°，
故选B．

点评 此题考查了圆周角定理和几何图形折叠的问题以及圆内接四边形的性质，解本题的关键是得出∠A'=110°．

练习册系列答案
相关题目
20．下列数中与$\sqrt{39}$最接近的是（　　）
A．5.5B．6C．6.5D．7
1．下列运算正确的是（　　）
A．2x2-x2=1B．2x•3x=6xC．（-x）3÷（-x）2=-xD．（2x）-2=$\frac{1}{4}$x2
18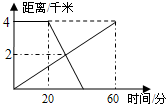．已知A，B两地相距4千米，上午8：00时，甲从A地步行到B地，8：20时乙从B地出发骑自行车到A地，甲、乙两人离A地的距离y（千米）与甲所用的时间x（分）之间的关系如图所示，则下列说法错误的是　（　　）
A．两人于8：30在途中相遇B．乙8：45到达A地
C．甲步行的速度是4千米/时D．乙骑车的速度是$\frac{1}{5}$千米/分
5．下列图形中，是中心对称图形，但不是轴对称图形的是（　　）
A．平行四边形B．线段C．等边三角形D．抛物线
15．不等式组$\left\{\begin{array}{l}{\frac{1}{2}x-1≤7-\frac{3}{2}x}\\{5x+2＞3（x-1）}\end{array}\right.$的所有整数解的和是m，则m的算术平方根在哪两个相邻的整数之间（　　）
A．2，3B．3，4C．1，2D．0，1
2．如图1，⊙O的直径AB=12，P是弦BC上一动点（与点B，C不重合），∠ABC=30°，过点P作PD⊥OP交⊙O于点D．

（1）如图2，当PD∥AB时，求PD的长；
（2）如图3，当$\widehat{DC}$=$\widehat{AC}$时，延长AB至点E，使BE=$\frac{1}{2}$AB，连接DE．
①求证：DE是⊙O的切线；
②求PC的长．
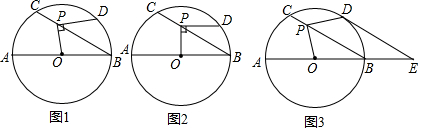
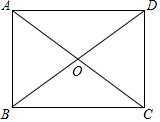19．如图所示，已知平行四边形ABCD，对角线AC，BD相交于点O，∠OBC=∠OCB．
（1）求证：平行四边形ABCD是矩形；
（2）请添加一个条件使矩形ABCD为正方形．
20．如图，小明为了测量一凉亭的高度AB（顶端A到水平地面BD的距离），在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE（DE=BC=0.5米，A、B、C三点共线），把一面镜子水平放置在平台上的点G处，测得CG=15米，然后沿直线CG后退到点E处，这时恰好在镜子里看到凉亭的顶端A，测得EG=3米，小明身高1.6米，则凉亭的高度AB约为（　　）
A．8.5米B．9米C．9.5米D．10米

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网