题目内容
11.已知,如图,AB是半圆O的直径,弦CD∥AB,动点P,Q分别在线段OC,CD上,且DQ=OP,AP的延长线与射线OQ相交于点E,与弦CD相交于点F(点F与点C,D不重合),AB=20,cos∠AOC=$\frac{4}{5}$,设OP=x,△CPF的面积为y.(1)求证:AP=OQ;
(2)求y关于x的函数关系式,并写出它的定义域;
(3)当△OPE是直角三角形时,求线段OP的长.
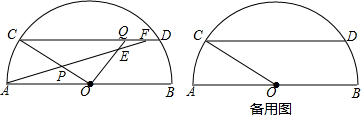
分析 (1)连接OD,证得△AOP≌△ODQ后即可证得AP=OQ;
(2)作PH⊥OA,根据cos∠AOC=$\frac{4}{5}$得到OH=$\frac{4}{5}$PO=$\frac{4}{5}$x,从而得到S△AOP=$\frac{1}{2}$AO•PH=3x,利用△PFC∽△PAO得当对应边的比相等即可得到函数解析式;
(3)分当∠POE=90°时、当∠OPE=90°时,当∠OEP=90°时三种情况讨论即可得到正确的结论.
解答  解:(1)连接OD,
解:(1)连接OD,
在△AOP和△ODQ中,
$\left\{\begin{array}{l}{AO=OD}\\{∠AOC=∠C=∠ODQ}\\{OP=DQ}\end{array}\right.$,
∴△AOP≌△ODQ,
∴AP=OQ;
(2)作PH⊥OA,
∵cos∠AOC=$\frac{4}{5}$,
∴OH=$\frac{4}{5}$PO=$\frac{4}{5}$x,
∴S△AOP=$\frac{1}{2}$AO•PH=3x,
又∵△PFC∽△PAO,
∴$\frac{y}{{S}_{△AOP}}$=$(\frac{CP}{PO})^{2}$=($\frac{10-x}{x}$)2,
整理得:y=$\frac{3{x}^{2}-60x+300}{x}$,
∵AP延长线与CD相交于点F,
∴CF≤CD=16,易知△CPF∽△OPA,
∴$\frac{CP}{x}=\frac{CF}{AO}$,
∴x的定义域为:$\frac{50}{13}$<x<10;
(3)当∠POE=90°时,CQ=$\frac{OC}{cos∠QCO}$=$\frac{25}{2}$,PO=DQ=CD-CQ=$\frac{7}{2}$(舍);
当∠OPE=90°时,PO=AO•cos∠COA=8;
当∠OEP=90°时,如图,由(1)知△AOP≌△ODQ,
∴∠APO=∠OQD,
∴∠AOQ=∠OQD=∠APO,
∵∠AOQ<90°,∠APO>90°(矛盾),
∴此种情况不存在,
∴线段OP的长为8.
点评 本题考查了圆的综合知识、相似三角形的判定及性质等知识,综合性较强,难度较大,特别是第三题的分类讨论更是本题的难点.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案| A. | 了解某种酸奶中钙的含量 | B. | 了解某班学生的课外作业时间 | ||
| C. | 公司招聘职员,对应聘人员的面试 | D. | 旅客上飞机前的安检 |
| A. | 2x-x=2 | B. | x•x4=2x5 | C. | x2y÷y=x2 | D. | (-2x)3=-6x3 |
| A. | $\sqrt{3}$ | B. | $\frac{1}{\sqrt{3}}$ | C. | -$\frac{1}{\sqrt{3}}$ | D. | -$\frac{1}{3}$ |
 如图,在平面直角坐标系中,△ABC三个顶点分别为A(-1,4)、B(-3,1)、C(-3,4),△A1B1C1是由△ABC绕某一点顺时针旋转得到的.
如图,在平面直角坐标系中,△ABC三个顶点分别为A(-1,4)、B(-3,1)、C(-3,4),△A1B1C1是由△ABC绕某一点顺时针旋转得到的.
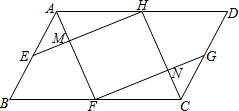 如图,在?ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,AF与EH交于点M,FG与CH交于点N.
如图,在?ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,AF与EH交于点M,FG与CH交于点N. 如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.