题目内容
2. 在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)在(1)的情况下,点M是第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;
(3)在(1)的情况下,若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.
分析 (1)由平行四边形ABOC绕点O顺时针旋转90°,得到平行四边形A′B′OC′,且点A的坐标是(0,4),可求得点A′的坐标,然后利用待定系数法即可求得经过点C、A、A′的抛物线的解析式;
(2)首先连接AA′,设直线AA′的解析式为:y=kx+b,利用待定系数法即可求得直线AA′的解析式,再设点M的坐标为:(x,-x2+3x+4),继而可得△AMA′的面积,继而求得答案;
(3)分别从BQ为边与BQ为对角线去分析求解即可求得答案.
解答 解:(1)∵平行四边形ABOC绕点O顺时针旋转90°,得到平行四边形A′B′OC′,且点A的坐标是(0,4),
∴点A′的坐标为:(4,0),
∵点A、C的坐标分别是(0,4)、(-1,0),抛物线经过点C、A、A′,
设抛物线的解析式为:y=ax2+bx+c,
∴$\left\{\begin{array}{l}{a-b+c=0}\\{c=4}\\{16a+4b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=3}\\{c=4}\end{array}\right.$,
∴此抛物线的解析式为:y=-x2+3x+4; (2)连接AA′,设直线AA′的解析式为:y=kx+b,
(2)连接AA′,设直线AA′的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}{b=4}\\{4k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=4}\end{array}\right.$,
∴直线AA′的解析式为:y=-x+4,
设点M的坐标为:(x,-x2+3x+4),
则S△AMA′=$\frac{1}{2}$×4×[-x2+3x+4-(-x+4)]=-2x2+8x=-2(x-2)2+8,
∴当x=2时,△AMA′的面积最大,最大值S△AMA′=8,
∴M的坐标为:(2,6);
(3)设点P的坐标为(x,-x2+3x+4),当P,N,B,Q构成平行四边形时,
∵平行四边形ABOC中,点A、C的坐标分别是(0,4)、(-1,0),
∴点B的坐标为(1,4),
∵点Q坐标为(1,0),P为抛物线上一动点,N为x轴上的一动点,
①当BQ为边时,PN∥BQ,PN=BQ,
∵BQ=4,
∴-x2+3x+4=±4,
当-x2+3x+4=4时,解得:x1=0,x2=3,
∴P1(0,4),P2(3,4);
当-x2+3x+4=-4时,解得:x3=$\frac{3+\sqrt{41}}{2}$,x4=$\frac{3-\sqrt{41}}{2}$,
∴P3($\frac{3+\sqrt{41}}{2}$,-4),P4($\frac{3-\sqrt{41}}{2}$,-4);
②当BQ为对角线时,BP∥QN,BP=QN,此时P与P1,P2重合;
综上可得:点P的坐标为:P1(0,4),P2(3,4),P3($\frac{3+\sqrt{41}}{2}$,-4),P4($\frac{3-\sqrt{41}}{2}$,-4);
如图2,当这个平行四边形为矩形时,点N的坐标为:(0,0)或(3,0).
点评 此题属于二次函数的综合题,考查了待定系数法求函数解析式的知识、平行四边形的性质以及三角形面积问题.掌握分类讨论思想的应用是解此题的关键.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案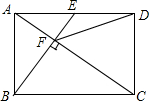 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$.
其中正确的结论有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -3 | D. | 3 |
