题目内容
12.某公司今年如果用原线下销售方式销售一产品,每月的销售额可达100万元.由于该产品供不应求,公司计划于3月份开始全部改为线上销售,这样,预计今年每月的销售额y(万元)与月份x(月)之间的函数关系的图象如图1中的点状图所示(5月及以后每月的销售额都相同),而经销成本p(万元)与销售额y(万元)之间函数关系的图象图2中线段AB所示.
(1)求经销成本p(万元)与销售额y(万元)之间的函数关系式;
(2)分别求该公司3月,4月的利润;
(3)问:把3月作为第一个月开始往后算,最早到第几个月止,该公司改用线上销售后所获得利润总额比同期用线下方式销售所能获得的利润总额至少多出200万元?(利润=销售额-经销成本)
分析 (1)设p=ky+b,(100,60),(200,110)代入即可解决问题.
(2)根据利润=销售额-经销成本,即可解决问题.
(3)设最早到第x个月止,该公司改用线上销售后所获得利润总额比同期用线下方式销售所能获得的利润总额至少多出200万元,列出不等式即可解决问题.
解答 解:(1)设p=ky+b,(100,60),(200,110)代入得$\left\{\begin{array}{l}{100k+b=60}\\{200k+b=110}\end{array}\right.$解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=10}\end{array}\right.$,
∴p=$\frac{1}{2}$y+10.
(2)∵y=150时,p=85,∴三月份利润为150-85=65万元.
∵y=175时,p=97.5,∴四月份的利润为175-97.5=77.5万元.
(3)设最早到第x个月止,该公司改用线上销售后所获得利润总额比同期用线下方式销售所能获得的利润总额至少多出200万元
∵5月份以后的每月利润为90万元(y=200,求得p=110,200-110=90),
∴65+77.5+90(x-2)-40x≥200,
∴x≥4.75,
∴最早到第5个月止,该公司改用线上销售后所获得利润总额比同期用线下方式销售所能获得的利润总额至少多出200万元.
点评 本题考查一次函数的应用、待定系数法、不等式等知识,解题的关键是构建一次函数解决问题,搞清楚利润=销售额-经销成本,属于中考常考题型.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
3. 如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
 如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{8\sqrt{13}}{13}$ | D. | $\frac{12\sqrt{13}}{13}$ |
 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5). 如图是一个正方体被截去一个直三棱柱得到的几何体,则该几何体的左视图是( )
如图是一个正方体被截去一个直三棱柱得到的几何体,则该几何体的左视图是( )



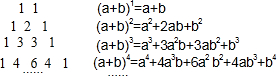 我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”.这个三角形给出了(a+b)n(n=1,2,3,4…)的展开式的系数规律(按a的次数由大到小的顺序):
我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”.这个三角形给出了(a+b)n(n=1,2,3,4…)的展开式的系数规律(按a的次数由大到小的顺序):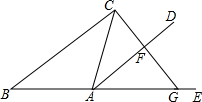 如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE.
如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE.
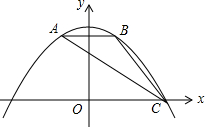 如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0,$\frac{9}{4}$),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0,$\frac{9}{4}$),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上. 在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.