Question

17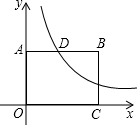．如图，四边形OABC为矩形，点B（4，3），双曲线y=$\frac{k}{x}$（x＞0）经过AB的中点D．
（1）求k的值；
（2）P是双曲线y=$\frac{k}{x}$（x＞0）上的一个动点，过P分别作PM⊥直线AB于M，PN⊥直线BC于N，若四边形PMBN为正方形，求P点坐标．

Answer 1

分析 （1）根据题意求得D的坐标，然后根据待定系数法即可求得；
（2）设正方形PMBN的边长为a，则P（4-a，3-a），然后代入解析式得到（4-a）（3-a）=6，解方程即可求得．

解答 解：（1）∵四边形OABC为矩形，点B（4，3），
∴D（2，3），
∵双曲线y=$\frac{k}{x}$（x＞0）经过AB的中点D，
∴k=2×3=6；
（2）设正方形PMBN的边长为a，则P（4-a，3-a），
∵P是双曲线y=$\frac{k}{x}$（x＞0）上的一个动点，
∴（4-a）（3-a）=6，
解得a=1或a=6（舍去），
∴P（3，2）

点评 本题考查了待定系数法求一次函数的解析式，正方形的性质，矩形的性质，熟练掌握性质是本题的关键．