题目内容
9．已知抛物线y=（x-1）2+a-1的顶点A在直线y=-x+3上，直线y=-x+3与x轴的交点为B，求△AOB的面积（O为坐标原点）．分析 可将抛物线的对称轴即顶点A的横坐标代入直线y=-x+3中，即可求出A点的坐标，然后根据直线的解析式再求出B点的坐标，进而可根据OB和A点的纵坐标的绝对值求出△AOB的面积．
解答 解：由题意可知：当x=1时，直线y=-x+3的值为：
y=-1+3=2，
因此A点的坐标为（1，2）
当y=0时，0=-x+3，x=3，
因此B点的坐标为（3，0）
∴△AOB的面积为：S=$\frac{1}{2}$×3×2=3．
点评 本题考查了一次函数的应用，二次函数解析式的确定、图形的面积求法、函数图象交点等知识及综合应用知识、解决问题的能力．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
20．
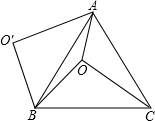如图，O是等边△ABC内一点，OA=3，OB=4，OC=5，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：
①△BO′A可以由△BOC绕点B逆时针旋转60°得到；
②点O与O′的距离为4；
③四边形AO BO′的面积为6+3$\sqrt{3}$
④∠AOB=150°；
⑤S△AOC+S△AOB=6+$\frac{9\sqrt{3}}{4}$．
其中正确的结论是（ ）
如图，O是等边△ABC内一点，OA=3，OB=4，OC=5，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：①△BO′A可以由△BOC绕点B逆时针旋转60°得到；
②点O与O′的距离为4；
③四边形AO BO′的面积为6+3$\sqrt{3}$
④∠AOB=150°；
⑤S△AOC+S△AOB=6+$\frac{9\sqrt{3}}{4}$．
其中正确的结论是（ ）
| A． | ②③④⑤ | B． | ①③④⑤ | C． | ①②③⑤ | D． | ①②④⑤ |
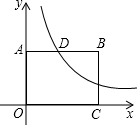如图，四边形OABC为矩形，点B（4，3），双曲线y=$\frac{k}{x}$（x＞0）经过AB的中点D．
4．
如图，AB是⊙O的直径，点C在⊙O上，P是AB上任意一点，则∠C的最大值为（ ）
如图，AB是⊙O的直径，点C在⊙O上，P是AB上任意一点，则∠C的最大值为（ ）| A． | 90° | B． | 60° | C． | 45° | D． | 30° |
如图，是由五个边长为2cm的小立方块搭成的几何体，一只蚂蚁想从A沿着这个几何体的表面爬到点B，它要爬行的最短路程应为2$\sqrt{5}$cm．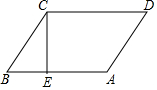
如图，平行四边形ABCD，AB=CD=9，AD=BC=5，（AB∥CD，AD∥BC），CE⊥AB于E，并且BE=3，CE=4．
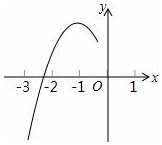已知抛物线y=ax2+bx+c的顶点为D（-1，3），与x轴的一个交点在（-3，0）和（-2，0）之间，其部分图象如图，则以下结论：