题目内容
12. 如图,在?ABCD中,以A为圆心,AB为半径作圆,分别交AD,BC于点F,G,延长BA交⊙A于点E,且∠B=50°,求点E,且∠B=50°,求$\widehat{EG}$的度数.
如图,在?ABCD中,以A为圆心,AB为半径作圆,分别交AD,BC于点F,G,延长BA交⊙A于点E,且∠B=50°,求点E,且∠B=50°,求$\widehat{EG}$的度数.
分析 连接AG,先根据平行线的性质得出∠EAF及∠BAD的度数,再由等腰三角形的性质得出∠BAG的度数,进而可得出∠GAF的度数,据此可得出结论.
解答  解:连接AG,
解:连接AG,
∵四边形ABCD是平行四边形,
∴AD∥BC.
∵∠B=50°,
∴∠EAF=50°,∠BAD=180°-50°=130°.
∵AB=AG,
∴∠BAG=180°-2∠B=180°-100°=80°,
∴∠GAF=130°-80°=50°,
∴∠EAF+∠GAF=50°+50°=100°,
∴$\widehat{EG}$=100°.
点评 本题考查的是圆心角、弧、弦的关系,熟知弧的度数等于此弧所对圆心角的度数是解答此题的关键.

练习册系列答案
相关题目
20.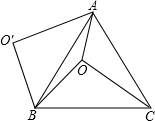 如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
①△BO′A可以由△BOC绕点B逆时针旋转60°得到;
②点O与O′的距离为4;
③四边形AO BO′的面积为6+3$\sqrt{3}$
④∠AOB=150°;
⑤S△AOC+S△AOB=6+$\frac{9\sqrt{3}}{4}$.
其中正确的结论是( )
 如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;
②点O与O′的距离为4;
③四边形AO BO′的面积为6+3$\sqrt{3}$
④∠AOB=150°;
⑤S△AOC+S△AOB=6+$\frac{9\sqrt{3}}{4}$.
其中正确的结论是( )
| A. | ②③④⑤ | B. | ①③④⑤ | C. | ①②③⑤ | D. | ①②④⑤ |
7.如图,不是位似图形的有( )

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4. 如图,AB是⊙O的直径,点C在⊙O上,P是AB上任意一点,则∠C的最大值为( )
如图,AB是⊙O的直径,点C在⊙O上,P是AB上任意一点,则∠C的最大值为( )
 如图,AB是⊙O的直径,点C在⊙O上,P是AB上任意一点,则∠C的最大值为( )
如图,AB是⊙O的直径,点C在⊙O上,P是AB上任意一点,则∠C的最大值为( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
8.如图四个图形中,是轴对称图形的有( )个


| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
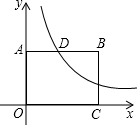 如图,四边形OABC为矩形,点B(4,3),双曲线y=$\frac{k}{x}$(x>0)经过AB的中点D.
如图,四边形OABC为矩形,点B(4,3),双曲线y=$\frac{k}{x}$(x>0)经过AB的中点D.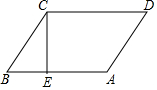 如图,平行四边形ABCD,AB=CD=9,AD=BC=5,(AB∥CD,AD∥BC),CE⊥AB于E,并且BE=3,CE=4.
如图,平行四边形ABCD,AB=CD=9,AD=BC=5,(AB∥CD,AD∥BC),CE⊥AB于E,并且BE=3,CE=4.