题目内容
4.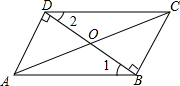 如图,△ABD和△CDB是两块形状、大小相同的三角尺,它们较长的直角边靠在一起(即重合在线段BD上),∠1=∠2=30°,∠ADB=∠CBD=90°,AD=8$\sqrt{3}$cm,连接AC,AC与BD相交于O点.求AC的长度.
如图,△ABD和△CDB是两块形状、大小相同的三角尺,它们较长的直角边靠在一起(即重合在线段BD上),∠1=∠2=30°,∠ADB=∠CBD=90°,AD=8$\sqrt{3}$cm,连接AC,AC与BD相交于O点.求AC的长度.
分析 易证四边形ABCD是平行四边形,则AO=CO,BO=DO,由∠1=30°,AD=8$\sqrt{3}$cm,可知AB=16$\sqrt{3}$cm,根据勾股定理BD=24cm,所以OD=12cm,在Rt△ADO中,AO=$\sqrt{A{D}^{2}+D{O}^{2}}$,于是AC=2AO.
解答 解:∵△ABD≌△CDB,
∴AD=BC,
∵∠ADB=∠CBD=90°,
∴AD∥BC,
∴四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵∠1=30°,AD=8$\sqrt{3}$cm,
∴AB=16$\sqrt{3}$cm,
在Rt△ABD中,
BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=24cm,
∴OD=12cm,
在Rt△ADO中,
AO=$\sqrt{A{D}^{2}+D{O}^{2}}$=4$\sqrt{21}$,
∴AC=2AO=8$\sqrt{21}$.
点评 本题主要考查了平行四边形的判定与性质、全等三角形的判定与性质、直角三角形的性质,解决此题的关键是把求AC转化为先求AC的一般AO,这样容易发现用勾股定理即可解决问题.

练习册系列答案
相关题目
12.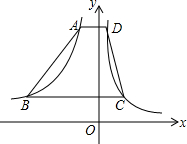 如图,在横跨第一、二象限的梯形ABCD中,AD∥BC∥x轴,AD=1,BC=4,它的高为4,四个顶点都在反比例函数的图象上,则关于A,B两点坐标说法错误的是( )
如图,在横跨第一、二象限的梯形ABCD中,AD∥BC∥x轴,AD=1,BC=4,它的高为4,四个顶点都在反比例函数的图象上,则关于A,B两点坐标说法错误的是( )
 如图,在横跨第一、二象限的梯形ABCD中,AD∥BC∥x轴,AD=1,BC=4,它的高为4,四个顶点都在反比例函数的图象上,则关于A,B两点坐标说法错误的是( )
如图,在横跨第一、二象限的梯形ABCD中,AD∥BC∥x轴,AD=1,BC=4,它的高为4,四个顶点都在反比例函数的图象上,则关于A,B两点坐标说法错误的是( )| A. | A点的横坐标是-$\frac{3}{5}$,B点的横坐标是-3 | |
| B. | A点的横坐标是-$\frac{3}{5}$,B点的纵坐标是$\frac{4}{3}$ | |
| C. | A点的纵坐标是$\frac{16}{3}$,B点的横坐标是-3 | |
| D. | A点的纵坐标是$\frac{16}{3}$,B点的纵坐标是$\frac{4}{3}$ |
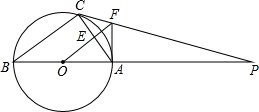 如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF;
如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF; 如图,△ABC的角平分线AD、BE相交于点P.∠ABC是直角,∠C=60°,请你判断并写出PE与PD之间的数量关系,并说明理由.
如图,△ABC的角平分线AD、BE相交于点P.∠ABC是直角,∠C=60°,请你判断并写出PE与PD之间的数量关系,并说明理由.
 如图所示,已知在△ABC中,∠ABC=90°,AB=BC,AE是∠A的平分线,CD⊥AE于点D,求证:CD=$\frac{1}{2}$AE.
如图所示,已知在△ABC中,∠ABC=90°,AB=BC,AE是∠A的平分线,CD⊥AE于点D,求证:CD=$\frac{1}{2}$AE.