题目内容
9. 如图,△ABC的角平分线AD、BE相交于点P.∠ABC是直角,∠C=60°,请你判断并写出PE与PD之间的数量关系,并说明理由.
如图,△ABC的角平分线AD、BE相交于点P.∠ABC是直角,∠C=60°,请你判断并写出PE与PD之间的数量关系,并说明理由.
分析 PE=PD,理由为:过P作PF垂直于AC,PG垂直于BC,由∠PDG为△ADC的一个外角,根据三角形的一个外角等于与它不相邻的两内角之和,得到∠PDG=∠C+∠CAD,又∠CAB=30°,AD为∠CAB的平分线得到∠CAD=$\frac{1}{2}$∠CAB,求出∠PDG的度数,同理∠PEF是△ABE的一个外角,即可求出∠PEF的度数,发现两角相等,再由垂直得到一对直角相等,根据角平分线的性质可知PF=PG,根据“AAS”即可得到三角形PEF与三角形PDG全等,根据全等三角形的对应边相等即可得证.
解答 PE=PD.
证明:∵∠ABC=90°,∠C=60°,
∴∠CAB=30°,
∵AD平分∠BAC,BE平分∠ABC,
∴∠CAD=∠BAD=$\frac{1}{2}$∠CAB=15°,∠ABE=∠CBE=$\frac{1}{2}$∠ABC=45°,
过点P作PF⊥AC,PG⊥BC,垂足分别为F、G,
则∠PFE=∠PGD=90°,
∵∠PDG为△ADC的一个外角,
∴∠PDG=∠C+∠CAD=60°+$\frac{1}{2}$∠CAB=60°+15°=75°,
∵∠PEF是△ABE的一个外角,
∴∠PEF=∠CAB+∠ABE=30°+$\frac{1}{2}$∠CBA=30°+45°=75°,
∴∠PEF=∠PDG,
∵PF⊥AC,PG⊥BC,
∴∠PFE=∠PGD=90°,
根据角平分线的性质可知:PF=PG,
在△PFE和△PGD中,
$\left\{\begin{array}{l}{∠PFE=∠PGD}\\{∠PEF=∠PDG}\\{PF=PG}\end{array}\right.$
∴△PFE≌△PGD,
∴PE=PD.
点评 此题综合考查了角平分线性质定理、全等三角形的判定与性质以及三角形的外角性质.遇到角平分线常经过角平分线上的点作角两边的垂线,得到两垂线段的长相等;本题先实验猜想,再探索证明,其目的是考查学生提出问题,解决问题的能力.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 组别 | 听写正确的个数x | 组中值 |
| A | 0≤x<8 | 4 |
| B | 8≤x<16 | 12 |
| C | 16≤x<24 | 20 |
| D | 24≤x<32 | 28 |
| E | 32≤x<40 | 36 |
(2)若把每组听写正确的个数用这组数据的组中值代替,则被抽查学生听写正确的个数的平均数是多少?
(3)该校共有1500名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.

| A. | 最小是1,最大是5 | B. | 最小是1,无最大值 | ||
| C. | 最小是3,最大是9 | D. | 最小是1,最大是9 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
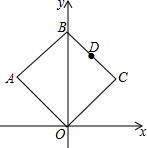 如图,正方形OABC的对角线OB在y轴正半轴上,且OB=4,点A在第二象限,点C在第一象限,点D是BC的中点,则点D的坐标是(1,3).
如图,正方形OABC的对角线OB在y轴正半轴上,且OB=4,点A在第二象限,点C在第一象限,点D是BC的中点,则点D的坐标是(1,3).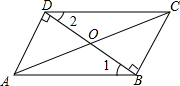 如图,△ABD和△CDB是两块形状、大小相同的三角尺,它们较长的直角边靠在一起(即重合在线段BD上),∠1=∠2=30°,∠ADB=∠CBD=90°,AD=8$\sqrt{3}$cm,连接AC,AC与BD相交于O点.求AC的长度.
如图,△ABD和△CDB是两块形状、大小相同的三角尺,它们较长的直角边靠在一起(即重合在线段BD上),∠1=∠2=30°,∠ADB=∠CBD=90°,AD=8$\sqrt{3}$cm,连接AC,AC与BD相交于O点.求AC的长度.