题目内容
14.计算题(1)先化简,再求值:$\frac{{a}^{2}+ab}{{a}^{2}+2ab{+b}^{2}}$-(a-b)÷$\frac{{a}^{2}-{b}^{2}}{b}$,其中a=sin45°,b=cos30°;
(2)若关于x的方程$\frac{x-a}{x-1}$-$\frac{3}{x}$=1无解,求a的值.
分析 (1)原式第二项利用除法法则变形,约分后利用同分母分式的减法法则计算,约分得到最简结果,把a与b的值代入计算即可求出值;
(2)分式方程去分母转化为整式方程,由分式方程无解求出x的值,代入计算即可求出a的值.
解答 解:(1)原式=$\frac{a(a+b)}{(a+b)^{2}}$-(a-b)•$\frac{b}{(a+b)(a-b)}$=$\frac{a}{a+b}$-$\frac{b}{a+b}$=$\frac{a-b}{a+b}$,
当a=sin45°=$\frac{\sqrt{2}}{2}$,b=cos30°=$\frac{\sqrt{3}}{2}$时,原式=$\frac{\frac{\sqrt{2}}{2}-\frac{\sqrt{3}}{2}}{\frac{\sqrt{2}}{2}+\frac{\sqrt{3}}{2}}$=$\frac{\sqrt{2}-\sqrt{3}}{\sqrt{2}+\sqrt{3}}$=-(5-2$\sqrt{6}$)=2$\sqrt{6}$-5;
(2)去分母得:x2-ax-3x+3=x2-x,
解得:x=$\frac{3}{a+2}$,
由分式方程无解,得到x(x-1)=0,即x=0或x=1,
若x=0,a无解;若x=1,解得:a=1.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.在实数-4、0、2、5中,最小的实数是( )
| A. | -4 | B. | 0 | C. | 2 | D. | 5 |
 有理数a,b,c在数轴上对应的点如:用“>”或“<”号填空
有理数a,b,c在数轴上对应的点如:用“>”或“<”号填空
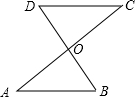 已知:如图,AC和BD相交于点O,OA=OC,OB=OD.
已知:如图,AC和BD相交于点O,OA=OC,OB=OD.
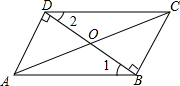 如图,△ABD和△CDB是两块形状、大小相同的三角尺,它们较长的直角边靠在一起(即重合在线段BD上),∠1=∠2=30°,∠ADB=∠CBD=90°,AD=8$\sqrt{3}$cm,连接AC,AC与BD相交于O点.求AC的长度.
如图,△ABD和△CDB是两块形状、大小相同的三角尺,它们较长的直角边靠在一起(即重合在线段BD上),∠1=∠2=30°,∠ADB=∠CBD=90°,AD=8$\sqrt{3}$cm,连接AC,AC与BD相交于O点.求AC的长度.