题目内容
14. 如图所示,已知在△ABC中,∠ABC=90°,AB=BC,AE是∠A的平分线,CD⊥AE于点D,求证:CD=$\frac{1}{2}$AE.
如图所示,已知在△ABC中,∠ABC=90°,AB=BC,AE是∠A的平分线,CD⊥AE于点D,求证:CD=$\frac{1}{2}$AE.
分析 延长CD交AB的延长线于F,由ASA证明△ACD≌△AFD,得出CD=DF=$\frac{1}{2}$CF,再由ASA证明△BCF≌△BAE,得出CF=AE,即可得出结论.
解答 证明:延长CD交AB的延长线于F,如图所示: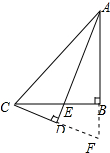 ∵CD⊥AD,
∵CD⊥AD,
∴∠ADC=∠ADF=90°,
∵AE是∠A的平分线,
∴∠CAD=∠FAD,
在△ACD和△AFD中,$\left\{\begin{array}{l}{∠ADC=∠ADF}&{\;}\\{AD=AD}&{\;}\\{∠CAD=∠FAD}&{\;}\end{array}\right.$,
∴△ACD≌△AFD(ASA),
∴CD=DF=$\frac{1}{2}$CF,
∵∠ABC=90°,
∴∠CBF=90°,
∴∠F+∠BCF=90°,
∵∠F+∠BAE=90°,
∴∠BCF=∠BAE,
在△BCF和△BAE中,$\left\{\begin{array}{l}{∠CBF=∠ABE=90°}&{\;}\\{BC=BA}&{\;}\\{∠BCF=∠BAE}&{\;}\end{array}\right.$,
∴△BCF≌△BAE(ASA),
∴CF=AE,
∴CD=$\frac{1}{2}$AE.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定与性质、角的平分线;熟练掌握等腰直角三角形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
9.下列代数运算正确的是( )
| A. | (x3)2=x5 | B. | (2x)2=2x2 | C. | (x+1)2=x2+1 | D. | x3•x2=x5 |
19.将点M(-1,-5)向右平移3个单位长度得到点N,则点N所处的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.期中考试后,甲说:“我组成绩是86分的同学最多”,乙说:“我组9人成绩排在最中间的恰好也是86分”,两位同学的话反映的统计量分别为( )
| A. | 众数和中位数 | B. | 平均数和中位数 | C. | 众数和方差 | D. | 众数和平均数 |
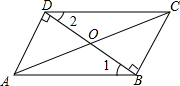 如图,△ABD和△CDB是两块形状、大小相同的三角尺,它们较长的直角边靠在一起(即重合在线段BD上),∠1=∠2=30°,∠ADB=∠CBD=90°,AD=8$\sqrt{3}$cm,连接AC,AC与BD相交于O点.求AC的长度.
如图,△ABD和△CDB是两块形状、大小相同的三角尺,它们较长的直角边靠在一起(即重合在线段BD上),∠1=∠2=30°,∠ADB=∠CBD=90°,AD=8$\sqrt{3}$cm,连接AC,AC与BD相交于O点.求AC的长度.