题目内容
19.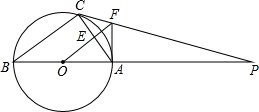 如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF;
如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF;(1)判断AF与⊙O的位置关系并说明理由.
(2)若⊙O的半径为4,AF=3,求AC的长.
分析 (1)连接OC,先证出∠3=∠2,由SAS证明△OAF≌△OCF,得对应角相等∠OAF=∠OCF,再根据切线的性质得出∠OCF=90°,证出∠OAF=90°,即可得出结论;
(2)先由勾股定理求出OF,再由三角形的面积求出AE,根据垂径定理得出AC=2AE.
解答 (1)证明:连接OC,如图所示: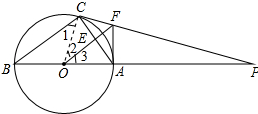
∵AB是⊙O直径,
∴∠BCA=90°,
∵OF∥BC,
∴∠AEO=90°,∠1=∠2,∠B=∠3,
∴OF⊥AC,
∵OC=OA,
∴∠B=∠1,
∴∠3=∠2,
在△OAF和△OCF中,
$\left\{\begin{array}{l}{OA=OC}\\{∠3=∠2}\\{OF=OF}\end{array}\right.$,
∴△OAF≌△OCF(SAS),
∴∠OAF=∠OCF,
∵PC是⊙O的切线,
∴∠OCF=90°,
∴∠OAF=90°,
∴FA⊥OA,
∴AF是⊙O的切线;
(2)∵⊙O的半径为4,AF=3,∠OAF=90°,
∴OF=$\sqrt{A{F}^{2}+O{A}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5
∵FA⊥OA,OF⊥AC,
∴AC=2AE,△OAF的面积=$\frac{1}{2}$AF•OA=$\frac{1}{2}$OF•AE,
∴3×4=5×AE,
解得:AE=$\frac{12}{5}$,
∴AC=2AE=$\frac{24}{5}$.
点评 本题考查了切线的判定、全等三角形的判定与性质、勾股定理、垂径定理以及三角形面积的计算;熟练掌握切线的判定,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
10.下列计算正确的是( )
| A. | -|-2|=-2 | B. | 20=0 | C. | 2-1-=-2 | D. | $\sqrt{4}$=±2 |
7.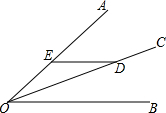 如图,D是∠AOB平分线OC上一点,过点D作DE∥OB交射线OA于点E,已知∠BOD=25°,则∠OED=( )
如图,D是∠AOB平分线OC上一点,过点D作DE∥OB交射线OA于点E,已知∠BOD=25°,则∠OED=( )
 如图,D是∠AOB平分线OC上一点,过点D作DE∥OB交射线OA于点E,已知∠BOD=25°,则∠OED=( )
如图,D是∠AOB平分线OC上一点,过点D作DE∥OB交射线OA于点E,已知∠BOD=25°,则∠OED=( )| A. | 40° | B. | 50° | C. | 130° | D. | 150° |
9.下列代数运算正确的是( )
| A. | (x3)2=x5 | B. | (2x)2=2x2 | C. | (x+1)2=x2+1 | D. | x3•x2=x5 |
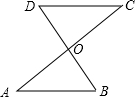 已知:如图,AC和BD相交于点O,OA=OC,OB=OD.
已知:如图,AC和BD相交于点O,OA=OC,OB=OD.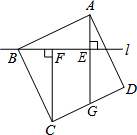 如图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.
如图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.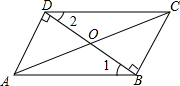 如图,△ABD和△CDB是两块形状、大小相同的三角尺,它们较长的直角边靠在一起(即重合在线段BD上),∠1=∠2=30°,∠ADB=∠CBD=90°,AD=8$\sqrt{3}$cm,连接AC,AC与BD相交于O点.求AC的长度.
如图,△ABD和△CDB是两块形状、大小相同的三角尺,它们较长的直角边靠在一起(即重合在线段BD上),∠1=∠2=30°,∠ADB=∠CBD=90°,AD=8$\sqrt{3}$cm,连接AC,AC与BD相交于O点.求AC的长度.