题目内容
6.观察以下一系列等式:①21-20=2-1=20; ②22-21=4-2=21;
③23-22=8-4=22; ④24-23=16-8=23;…
(1)请按这个顺序仿照前面的等式写出第④个等式;24-23=16-8=23
(2)若字母n代表第n个等式,请用字母n表示上面所发现的规律:2n-2n-1=2n-1;
(3)请利用上述规律计算:20+21+22+23+…+21000.
分析 (1)根据已知等式的指数与序数的关系即可得;
(2)观察各等式得到2的相邻两个正整数幂的差等于2的较小的正整数次幂,即2n-2n-1=2n-1(n为正整数);
(3)由(1)(2)得20=21-20,21=22-21,22=22-21,…,21000=21001-21000,代入待求等式,两两相消即可得.
解答 解:(1)∵①21-20=2-1=20;
②22-21=4-2=21;
③23-22=8-4=22;
∴第④个等式为:24-23=16-8=23,
故答案为:24-23=16-8=23;
(2)由(1)知,第n个等式为:2n-2n-1=2n-1,
故答案为:2n-2n-1=2n-1;
(3)∵20=21-20,21=22-21,22=22-21,…,21000=21001-21000,
∴20+21+22+23+…+21000=(21-20)+(22-21)+(22-21)+…+(21001-21000)=21001-20=21001-1.
点评 本题主要考查数字的变化类,解决此类问题的关键是找到序号和变化数字的关系,另外题目涉及证明和运算,对学生的考查能力有了更高的要求,题目整体艰难,适合课后培优训练.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
16.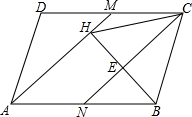 如图,已知点M、N分别为?ABCD的边CD、AB的中点,连接AM、CN.
如图,已知点M、N分别为?ABCD的边CD、AB的中点,连接AM、CN.
(1)证明:AM=CN;
(2)过点B作BH⊥AM于点H,交CN于点E,连接CH,判断线段CB、CH的数量关系,并说明理由.
 如图,已知点M、N分别为?ABCD的边CD、AB的中点,连接AM、CN.
如图,已知点M、N分别为?ABCD的边CD、AB的中点,连接AM、CN.(1)证明:AM=CN;
(2)过点B作BH⊥AM于点H,交CN于点E,连接CH,判断线段CB、CH的数量关系,并说明理由.
1.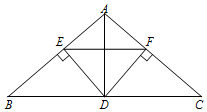 如图,在△ABC中,AB=AC,D是边BC上一点,DE⊥AB,DF⊥AC,垂足分别是E、F,△AEF∽△ABC.
如图,在△ABC中,AB=AC,D是边BC上一点,DE⊥AB,DF⊥AC,垂足分别是E、F,△AEF∽△ABC.
(1)求证:△AED≌△AFD;
(2)若BC=2AD,求证:四边形AEDF是正方形.
 如图,在△ABC中,AB=AC,D是边BC上一点,DE⊥AB,DF⊥AC,垂足分别是E、F,△AEF∽△ABC.
如图,在△ABC中,AB=AC,D是边BC上一点,DE⊥AB,DF⊥AC,垂足分别是E、F,△AEF∽△ABC.(1)求证:△AED≌△AFD;
(2)若BC=2AD,求证:四边形AEDF是正方形.
7.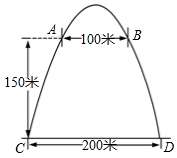 如图,拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,则拱门的最大高度( )
如图,拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,则拱门的最大高度( )
 如图,拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,则拱门的最大高度( )
如图,拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,则拱门的最大高度( )| A. | 100米 | B. | 150米 | C. | 200米 | D. | 300米 |
 如图,△ABC中,AB=AC=10,AD⊥BC于D,AD=8,求S△ABC.
如图,△ABC中,AB=AC=10,AD⊥BC于D,AD=8,求S△ABC. 在平面直角坐标系xOy中,抛物线y=ax2-4ax+4a-3(a≠0)的顶点为A.
在平面直角坐标系xOy中,抛物线y=ax2-4ax+4a-3(a≠0)的顶点为A.