题目内容
7.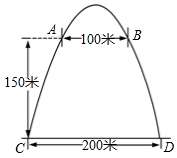 如图,拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,则拱门的最大高度( )
如图,拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,则拱门的最大高度( )| A. | 100米 | B. | 150米 | C. | 200米 | D. | 300米 |
分析 因为拱门是抛物线形,所以符合抛物线的性质,以CD的中垂线为y轴,CD所在的直线为x轴,可列出含有未知量的抛物线解析式,由A、B的坐标可求出抛物线的解析式,然后就变成求抛物线的顶点坐标的问题.
解答 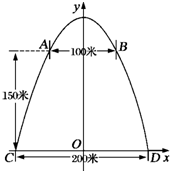 解:如图所示建立平面直角坐标系(以CD所在的直线为x轴,CD的垂直平分线为y轴建立直角坐标系),
解:如图所示建立平面直角坐标系(以CD所在的直线为x轴,CD的垂直平分线为y轴建立直角坐标系),
此时,抛物线与x轴的交点为C(-100,0),D(100,0),
设这条抛物线的解析式为y=a(x-100)(x+100),
∵抛物线经过点B(50,150),
可得 150=a(50-100)(50+100).
解得 a=-$\frac{1}{50}$,
∴y=-$\frac{1}{50}$(x-100)(x+100).
即 抛物线的解析式为y=-$\frac{1}{50}$x2+200
顶点坐标是(0,200)
∴拱门的最大高度为200米,
故选C.
点评 此题考查的二次函数在实际生活中的应用,根据题意正确的建立坐标轴可使问题简单化,数形结合,是一道基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
3.正方形具有而菱形不具备的性质是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | ||
| C. | 对角线平分一组对角 | D. | 对角线相等 |
 如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2=45°.
如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2=45°.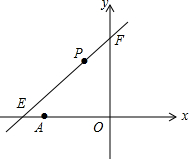 如图,直线l:y=kx+6与x轴、y轴分别相交于E、F,点E的坐标为(-9,0),点A的坐标为(-6,0),点P(x,y)是直线l上的一个动点.
如图,直线l:y=kx+6与x轴、y轴分别相交于E、F,点E的坐标为(-9,0),点A的坐标为(-6,0),点P(x,y)是直线l上的一个动点. 按下列要求在方格纸中画图:
按下列要求在方格纸中画图: