题目内容
18.计算 $\frac{3}{\sqrt{3}}$-$\sqrt{\frac{1}{3}}$的结果是$\frac{2\sqrt{3}}{3}$.分析 首先化成最简二次根式,然后把同类二次根式进行合并即可.
解答 解:$\frac{3}{\sqrt{3}}$-$\sqrt{\frac{1}{3}}$=$\frac{\sqrt{3}•\sqrt{3}}{\sqrt{3}}$-$\frac{\sqrt{3}}{3}$=$\sqrt{3}$-$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$,
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 此题主要考查了二次根式的加减,关键是掌握二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
3.正方形具有而菱形不具备的性质是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | ||
| C. | 对角线平分一组对角 | D. | 对角线相等 |
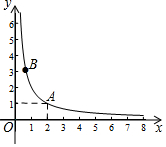 如图,在平面直角坐标系xOy中的第一象限内,反比例函数图象过点A(2,1)和另一动点B(x,y).
如图,在平面直角坐标系xOy中的第一象限内,反比例函数图象过点A(2,1)和另一动点B(x,y). 如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2=45°.
如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2=45°.