题目内容
10．
如图，O是矩形ABCD对角线的交点，DE∥AC，CE∥BD，试说明OE与CD互相垂直平分．
分析 已知OE与CD是四边形OCDE的对角线，且DE∥AC，CE∥BD，即：四边形OCED是平行四边形，要证明OE⊥CD，只需证明四边形OCED是菱形，由菱形的对角线互相垂直即可求解．
解答 证明：∵四边形ABCD是矩形，
∴AC=BD，OA=OC=OD=OB（矩形的对角线相等且互相平分），
又∵DE∥AC，CE∥BD，
∴四边形OCED是平行四边形，
又∵OC=OD，
∴四边形OCED是菱形，
∴OE⊥CD且OE与CD互相平分（菱形的对角线互相垂直平分）．
点评 本题考查矩形的性质和菱形的性质，即：矩形的对角线相等且互相平分；菱形的对角线互相垂直．
练习册系列答案
相关题目
20．
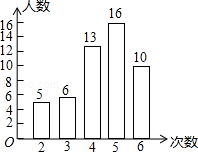我市开展了“寻找雷锋足迹”的活动，某中学为了了解八年级800名学生在“学雷锋活动月”中做好事的情况，随机调查了八年级50名学生在一个月内做好事的次数，并将所得数据绘制成统计图，估计该校八年级800名学生在“学雷锋活动月”中做好事不少于5次的人数有（ ）
我市开展了“寻找雷锋足迹”的活动，某中学为了了解八年级800名学生在“学雷锋活动月”中做好事的情况，随机调查了八年级50名学生在一个月内做好事的次数，并将所得数据绘制成统计图，估计该校八年级800名学生在“学雷锋活动月”中做好事不少于5次的人数有（ ）| A． | 384 | B． | 256 | C． | 160 | D． | 416 |
1．
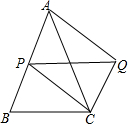如图，在△ABC中，∠BAC=45°，AB=AC=8，P为AB边上一动点，以PA、PC为边作平行四边形PAQC，则对角线PQ的最小值为（ ）
如图，在△ABC中，∠BAC=45°，AB=AC=8，P为AB边上一动点，以PA、PC为边作平行四边形PAQC，则对角线PQ的最小值为（ ）| A． | 6 | B． | 8 | C． | 2$\sqrt{2}$ | D． | 4$\sqrt{2}$ |
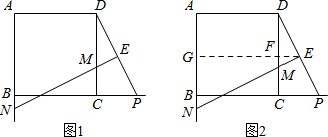
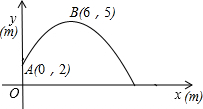在体育测试时，初三（2）班的高个子张成同学推铅球，已知铅球所经过的路线是抛物线y=ax2+bx+c的一部分（如图所示），且知铅球出手处A点的坐标为（0，2）（单位：m，后同），铅球路线中最高处B点的坐标为（6，5）
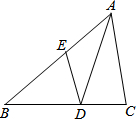如图，在△ABC中，AD是角平分线，点E在AB上，且DE∥CA．
如图，直线AB∥CD，与直线EF分别交于M，N，则图中与∠END相等的角（∠END除外）的个数为（ ）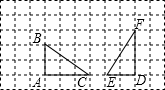
如图方格纸中△ABC绕着点A逆时针旋转90度，再向右平移6格可得到△DEF．