题目内容
18.数学课上,李老师出示了这样一道题目:如图1,正方形ABCD的边长为12,P为边BC延长线上的一点,E为DP的中点,DP的垂直平分线交边DC于M,交边AB的延长线于N.当CP=6时,EM与EN的比值是多少?经过思考,小明展示了一种正确的解题思路:过E作直线平行于BC交DC,AB分别于F,G,如图2,则可得:$\frac{DF}{FC}=\frac{DE}{EP}$,因为DE=EP,所以DF=FC.可求出EF和EG的值,进而可求得EM与EN的比值.
(1)请按照小明的思路写出求解过程.
(2)小东又对此题作了进一步探究,得出了DP=MN的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
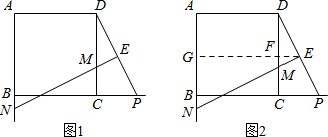
分析 (1)过E作EG∥BC交DC于F,交AB于点G,如图,由EF∥PC,可证明△DEF∽△DPC,利用相似比可得DF=$\frac{1}{2}$DC=6,EF=$\frac{1}{2}$PC=3,则EG=GF+EF=15,然后根据平行线分线段成比例,由FM∥GN得到$\frac{EM}{EN}$=$\frac{EF}{EG}$=$\frac{1}{5}$;
(2)作MH∥BC交AB于点H,如图2,则MH=CB=CD,先证明∠1=∠2,然后根据“ASA”可证明△DPC≌△MNH,从而得到DP=MN.
解答 (1)解:过E作EG∥BC交DC于F,交AB于点G,如图,
∵NE垂直平分DP,
∴DE=EP,
∵EF∥PC,
∴△DEF∽△DPC,
∴$\frac{DF}{DC}$=$\frac{EF}{PC}$=$\frac{DE}{DP}$=$\frac{1}{2}$
∴DF=$\frac{1}{2}$DC=6,EF=$\frac{1}{2}$PC=3,
∴EG=GF+EF=12+3=15,
∵FM∥GN,
∴$\frac{EM}{EN}$=$\frac{EF}{EG}$=$\frac{3}{15}$=$\frac{1}{5}$;
(2)结论正确.证明如下:
作MH∥BC交AB于点H,如图2,则MH=CB=CD,
∵NE⊥PD,
∴∠MED=90°,
∴∠2+∠DME=90°,
∵∠1+∠DME=90°,
∴∠1=∠2,
在△DPC和△MNH中,
$\left\{\begin{array}{l}{∠2=∠1}\\{DC=MH}\\{∠DCP=∠MHN}\end{array}\right.$,
∴△DPC≌△MNH,
∴DP=MN.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了正方形的性质和全等三角形的判定与性质.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
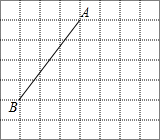 线段AB的端点在边长为1的正方形网格格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.
线段AB的端点在边长为1的正方形网格格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.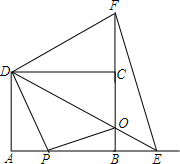 如图,矩形ABCD中,动点P从点A出发,沿线段AB以每秒2cm的速度向点B运动:同时动点Q从点B出发,沿线段BC以每秒1cm的速度向点C运动.当点P到达B点时,点Q同时停止,设运动时间为t秒.已知AD=6,且t=2时,PQ=2$\sqrt{5}$.
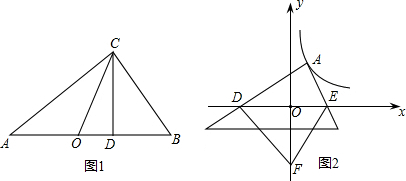
如图,矩形ABCD中,动点P从点A出发,沿线段AB以每秒2cm的速度向点B运动:同时动点Q从点B出发,沿线段BC以每秒1cm的速度向点C运动.当点P到达B点时,点Q同时停止,设运动时间为t秒.已知AD=6,且t=2时,PQ=2$\sqrt{5}$.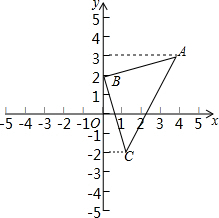 如图,利用关于坐标轴对称的点的坐标的特点,作出△ABC关于x轴对称的图形.
如图,利用关于坐标轴对称的点的坐标的特点,作出△ABC关于x轴对称的图形. 如图,O是矩形ABCD对角线的交点,DE∥AC,CE∥BD,试说明OE与CD互相垂直平分.
如图,O是矩形ABCD对角线的交点,DE∥AC,CE∥BD,试说明OE与CD互相垂直平分.