题目内容
11.顺次连结对角线互相垂直平分的四边形的各边中点,所组成的四边形是( )| A. | 矩形 | B. | 正方形 | C. | 菱形 | D. | 等腰梯形 |
分析 先证明四边形EFGH是平行四边形,再根据有一个角是直角的平行四边形是矩形判断.
解答  解:如图,∵四边形ABCD的对角线互相垂直平分,
解:如图,∵四边形ABCD的对角线互相垂直平分,
∴四边形ABCD是菱形,
∵菱形ABCD中,E、F、G、H分别是AB、BC、CD、AD的中点,
∴EH∥FG∥BD,EH=FG=$\frac{1}{2}$BD;EF∥HG∥AC,EF=HG=$\frac{1}{2}$AC,
故四边形EFGH是平行四边形,
又∵AC⊥BD,
∴EH⊥EF,∠HEF=90°
∴四边形EFGH是矩形.
故选:A.
点评 此题主要考查了菱形的性质,矩形的概念及三角形的中位线定理,正确把握相关性质是解题关键.

练习册系列答案
相关题目
1.若一组数据:2,-1,x,3的极差是5,则x的值为( )
| A. | 6 | B. | -2 | C. | 4 | D. | 4或-2 |
2. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )| A. | 55° | B. | 50° | C. | 45° | D. | 60° |
6.已知,3<m<6,且点A(m,y1),B($\frac{1}{3}$m+1,y2),C(2,y3)都在二次函数y=$\sqrt{5}$x2-2$\sqrt{5}$x+3的图象上,则下列说法正确的是( )
| A. | y2<y1<y3 | B. | y2<y3<y1 | C. | y3<y2<y1 | D. | y1<y3<y2 |
8.若点A(2,n)在x 轴上,则点B(n-2,n+l)在( )
| A. | 第一象限 | B. | 第三象限 | C. | 第四象限 | D. | 第二象限 |
 如图,已知过原点的直线与双曲线$y=\frac{k}{x}$(k>0)交于A、B两点,点A到x轴的距离是它到y轴距离的一半,点B的纵坐标为-2.
如图,已知过原点的直线与双曲线$y=\frac{k}{x}$(k>0)交于A、B两点,点A到x轴的距离是它到y轴距离的一半,点B的纵坐标为-2.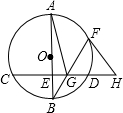 如图.AB为⊙O的直径,CD为⊙O的弦,且AB⊥CD于E,F为劣弧$\widehat{AD}$上一点,BF交CD于点G,过点F作⊙O的切线,交CD的延长线于H.
如图.AB为⊙O的直径,CD为⊙O的弦,且AB⊥CD于E,F为劣弧$\widehat{AD}$上一点,BF交CD于点G,过点F作⊙O的切线,交CD的延长线于H.