题目内容
1.观察下列等式:$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$将以上三个等式两边分别相加得:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$
(1)直接写出下式:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2015×2016}$的计算结果为$\frac{2015}{2016}$.
(2)探究并计算:$\frac{1}{2×4}$+$\frac{1}{4×6}$+…+$\frac{1}{2n×2(n+1)}$(其中n为正整数)
分析 (1)根据题意裂项求和即可得;
(2)根据$\frac{1}{2n×2(n+1)}$=$\frac{1}{2}$[$\frac{1}{2n}$-$\frac{1}{2(n+1)}$]裂项求解可得.
解答 解:(1)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2015×2016}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2015}$-$\frac{1}{2016}$
=1-$\frac{1}{2016}$
=$\frac{2015}{2016}$,
故答案为:$\frac{2015}{2016}$;
(2)原式=$\frac{1}{2}$[$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{6}$+…+$\frac{1}{2n}$-$\frac{1}{2(n+1)}$]
=$\frac{1}{2}$×[$\frac{1}{2}$-$\frac{1}{2(n+1)}$]
=$\frac{n}{4(n+1)}$
=$\frac{n}{4n+4}$.
点评 本题主要考查数字的变化规律,根据题意得出$\frac{1}{2n×2(n+1)}$=$\frac{1}{2}$[$\frac{1}{2n}$-$\frac{1}{2(n+1)}$]及裂项求和的方法是解题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
12.已知50°的圆心角所对的弧长是2.5πcm,则此弧所在圆的半径是( )
| A. | 6cm | B. | 7cm | C. | 8cm | D. | 9cm |
10.在函数$y=\frac{x-1}{{\sqrt{4-x}}}$中,自变量x的取值范围是( )
| A. | x≠4 | B. | x≤4 | C. | x<4 | D. | 1<x<4 |
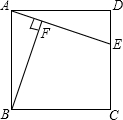 如图,已知点E是矩形ABCD的边CD上一点,BF⊥AE于点F,求证:△ABF∽△EAD.
如图,已知点E是矩形ABCD的边CD上一点,BF⊥AE于点F,求证:△ABF∽△EAD.