题目内容
12.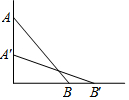 如图,一根长为a的竹竿AB斜靠在墙上,竹竿AB的倾斜角为α,当竹竿的顶端A下滑到点A'时,竹竿的另一端B向右滑到了点B',此时倾斜角为β.
如图,一根长为a的竹竿AB斜靠在墙上,竹竿AB的倾斜角为α,当竹竿的顶端A下滑到点A'时,竹竿的另一端B向右滑到了点B',此时倾斜角为β.(1)线段AA'的长为a(sinα-sinβ).
(2)当竹竿AB滑到A'B'位置时,AB的中点P滑到了P',位置,则点P所经过的路线长为$\frac{(α-β)πa}{360}$(两小题均用含a,α,β的代数式表示)
分析 (1)分别在在Rt△ABO中和在Rt△A′OB′中,求出OA、OA′即可解决问题.
(2)点P运动轨迹是弧,求出圆心角、半径利用弧长公式计算即可.
解答 解:(1)在Rt△ABO中,∵AB=a,∠ABO=α,
∴OA=AB•sinα=a•sinα,
在Rt△A′OB′中,同理可得OA′=a•sinβ,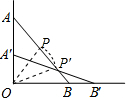
∴AA′=OA-OA′=a(sinα-sinβ).
故答案为a(sinα-sinβ).
(2)∵PA=PB,∠AOB=90°,
∴OP=PB=PA,
∴∠POB=α,同理可得∠P′OB=β,
∴∠POP′=α-β,
∴则点P所经过的路线长=$\frac{(α-β)π•\frac{1}{2}a}{180}$=$\frac{(α-β)•π•a}{360}$.
点评 本题考查勾股定理、轨迹、弧长公式、直角三角形斜边中线定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
3. 某几何体的主视图和左视图如图所示,则该几何体可能是( )
某几何体的主视图和左视图如图所示,则该几何体可能是( )
 某几何体的主视图和左视图如图所示,则该几何体可能是( )
某几何体的主视图和左视图如图所示,则该几何体可能是( )| A. | 长方体 | B. | 圆锥 | C. | 正方体 | D. | 球 |
 解不等式(组),并把第(2)的解集表示在数轴上.
解不等式(组),并把第(2)的解集表示在数轴上.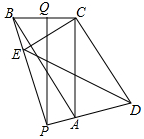 如图,在△ABC中,∠ACB=90°,BC=6,AC=8,将△ABC绕C点旋转一个角度到△DEC,直线AD,EB交于P点,Q是BC的中点,连PQ,在旋转过程中,求:
如图,在△ABC中,∠ACB=90°,BC=6,AC=8,将△ABC绕C点旋转一个角度到△DEC,直线AD,EB交于P点,Q是BC的中点,连PQ,在旋转过程中,求: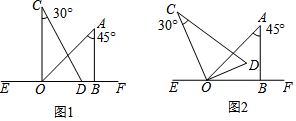
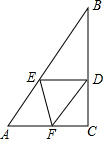 如图,Rt△ABC中,∠C=90°,∠B=30°,点D在BC上,BD=2CD,过D点作BC的垂线交AB于点E,BE=6cm,F为线段AC上一动点,则△DEF的周长最小值为9cm.
如图,Rt△ABC中,∠C=90°,∠B=30°,点D在BC上,BD=2CD,过D点作BC的垂线交AB于点E,BE=6cm,F为线段AC上一动点,则△DEF的周长最小值为9cm.