题目内容
11.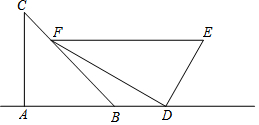 王生是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=4.求:
王生是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=4.求:(1)BD的长;
(2)△BDF的面积.
分析 (1)过点F作FM⊥AD于M,利用在直角三角形中,30°角所对的直角边等于斜边的一半和平行线的性质以及等腰直角三角形的性质即可求出BD的长.
(2)根据三角形面积公式可求△BDF的面积.
解答 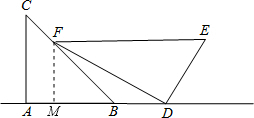 解:(1)过点F作FM⊥AD于M,
解:(1)过点F作FM⊥AD于M,
∵∠EDF=90°,∠E=60°,
∴∠EFD=30°,
∵DE=4,
∴EF=8,
∴DF=$\sqrt{E{F}^{2}-D{E}^{2}}$=4$\sqrt{3}$,
∵EF∥AD,
∴∠FDM=30°,
∴FM=$\frac{1}{2}$DF=2$\sqrt{3}$,
∴MD=$\sqrt{F{D}^{2}-F{M}^{2}}$=6,
∵∠C=45°,
∴∠MFB=∠B=45°,
∴FM=BM=2$\sqrt{3}$,
∴BD=DM-BM=6-2$\sqrt{3}$;
(2)△BDF的面积为$\frac{1}{2}$BD•FM=$\frac{1}{2}$×(6-2$\sqrt{3}$)×2$\sqrt{3}$=6$\sqrt{3}$-6.
点评 本题考查了勾股定理的运用、平行线的性质以及等腰直角三角形的性质,解题的关键是作垂直构造直角三角形,利用勾股定理求出DM的长.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
6.应用题
老张装修完新房,元旦期间又到苏宁电器购买冰箱、电视机和洗衣机三件家电,刚好该商场推出新年优惠活动,具体优惠情况如下表:
比如:买原价5000元的商品,实际花费3000+(5000-3000)(1-5%)-160=4740(元)
(1)已知老张购买的这三件家电原价合计为11500元,如果一次性支付,请求出他的实际花费;
(2)如果在该商场购买一件原价为x元的商品(x≤10000),请用含x的代数式表示实际花费;
(3)付款时,老张突然想到:如果一次性支付,虽然优惠率更高,却只能享受一次立减160元优惠,如果将这三件家电分开支付或者两件合并支付,另一件单独支付,就可以享受多次立减160元优惠,这样是否可能更加划算呢?已知老张购买的冰箱原价4800元,电视机原价4600元,洗衣机原价2100元,请你通过计算帮老张设计出最优惠的支付方案.
老张装修完新房,元旦期间又到苏宁电器购买冰箱、电视机和洗衣机三件家电,刚好该商场推出新年优惠活动,具体优惠情况如下表:
| 购物金额(原价) | 优惠率 |
| 不超过3000元的部分 | 无优惠 |
| 超过3000元但不超过10000元部分 | 5% |
| 超过10000元的部分 | 10% |
| 付款时,还可以享受单笔消费满2000元立减160元优惠 | |
(1)已知老张购买的这三件家电原价合计为11500元,如果一次性支付,请求出他的实际花费;
(2)如果在该商场购买一件原价为x元的商品(x≤10000),请用含x的代数式表示实际花费;
(3)付款时,老张突然想到:如果一次性支付,虽然优惠率更高,却只能享受一次立减160元优惠,如果将这三件家电分开支付或者两件合并支付,另一件单独支付,就可以享受多次立减160元优惠,这样是否可能更加划算呢?已知老张购买的冰箱原价4800元,电视机原价4600元,洗衣机原价2100元,请你通过计算帮老张设计出最优惠的支付方案.
3. 某几何体的主视图和左视图如图所示,则该几何体可能是( )
某几何体的主视图和左视图如图所示,则该几何体可能是( )
 某几何体的主视图和左视图如图所示,则该几何体可能是( )
某几何体的主视图和左视图如图所示,则该几何体可能是( )| A. | 长方体 | B. | 圆锥 | C. | 正方体 | D. | 球 |

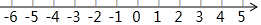 解不等式(组),并把第(2)的解集表示在数轴上.
解不等式(组),并把第(2)的解集表示在数轴上.