题目内容

10．设（3x-1）5=a5x5+a4x4+a3x3+a2x2+a1x+a0，求：
（1）a0的值为多少？
（2）a5+a4+a3+a2+a1+a0的值为多少？
（3）-a5+a4-a3+a2-a1+a0的值为多少？
（4）a5+a3+a1的值为多少？
（5）a4+a2的值为多少？

分析 （1）令x=0求出a0的值即可；
（2）令x=1求出所求式子的值即可；
（3）令x=-1求出所求式子的值即可；
（4）根据（2）和（3）的结果求出所求式子的值即可；
（5）由（1）、（2）、（4）的结果求出所求式子的值即可．

解答 解：（1）令x=0，得到a0=-1；
（2）令x=1，得到a5+a4+a3+a2+a1+a0=32①；
（3）令x=-1，得到-a5+a4-a3+a2-a1+a0=-512②；
（4）①-②得：2（a5+a3+a1）=544，即a5+a3+a1=272③；
（5）①-③得：a4+a2+a0=-240，即a4+a2=-239．

点评 此题考查了代数式求值，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
3．求下列各式中x的值
①（x-1）2-25=0                         
②5（x-3）3-40=0．
4．如图，等腰Rt△ABC中，∠ACB=90°，AC=BC=1，且AC边在直线a上，将△ABC绕点A顺时针旋转到位置①可得到点P1，此时AP1=$\sqrt{2}$；将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2，此时AP2=$\sqrt{2}$+1；将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时，AP3=$\sqrt{2}$+2…按此规律继续旋转，直至得到点P2016为止，则AP2016=1344+672$\sqrt{2}$．
1．简便计算：
①（+2.125）-（-1$\frac{2}{5}$）-3$\frac{1}{8}$+（-3$\frac{1}{3}$）+（-1.4）-1$\frac{1}{3}$
②-1.25×0.3+11.25×0.3-（-$\frac{4}{9}$-$\frac{5}{12}$+$\frac{1}{6}$）÷（-$\frac{1}{36}$）
5．阅读下面材料：
小明遇到这样一个问题：
如图1，△ABC中，∠A=90°，∠B=30°，点D，E分别在AB，BC上，且∠CDE=90°．当BE=2AD时，图1中是否存在与CD相等的线段？若存在，请找出并加以证明，若不存在，说明理由．
小明通过探究发现，过点E作AB的垂线EF，垂足为F，能得到一对全等三角形（如图2），从而将解决问题．

请回答：
（1）小明发现的与CD相等的线段是DE．
（2）证明小明发现的结论；
参考小明思考问题的方法，解决下面的问题：
（3）如图3，△ABC中，AB=AC，∠BAC=90°，点D在BC上，BD=2DC，点E在AD上，且∠BEC=135°，求$\frac{BE}{CE}$的值．
15．（1）如图，在x轴上，点A的坐标为3，点B的坐标为5，则AB的中点C的坐标为（4，0）

（2）在图中描出点A（2，1）和B（4，3），连结AB，找出AB的中点D并写出D的坐标．
（3）已知点M（a，b），N（c，d），根据以上规律直接写出MN的中点P的坐标．
2．已知：如图，AC、BD相交于点O，且AB=DC，AC=DB，则∠A与∠D相等吗？为什么？
19．如图，方格纸中每个小正方形的边长均为1，△A1B1C1和△A2B2C2的顶点都在方格纸的格点上．
（1）求△A1B1C1和△A2B2C2的面积比．
（2）点A1、D、E、F、G、H是△A1B1C1边上的6个格点，请在这6个格点中选取3个点作为三角形的顶点，使构成的三角形与△A2B2C2相似（要求写出2个符合条件的三角形，并分别在图1和图2中将相应三角形涂黑，不必说明理由）．
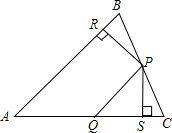20．如图所示，在△ABC中，P为BC上一点，PR⊥AB，垂足为R，PS⊥AC，垂足为S，AQ=PQ，PR=PS．下面三个结论：①AS=AR；②QP∥AR；③△BRP≌△CSP．上述结论中正确的是①②．（填序号）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网