题目内容
5.阅读下面材料:小明遇到这样一个问题:
如图1,△ABC中,∠A=90°,∠B=30°,点D,E分别在AB,BC上,且∠CDE=90°.当BE=2AD时,图1中是否存在与CD相等的线段?若存在,请找出并加以证明,若不存在,说明理由.
小明通过探究发现,过点E作AB的垂线EF,垂足为F,能得到一对全等三角形(如图2),从而将解决问题.
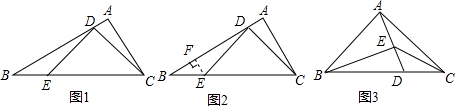
请回答:
(1)小明发现的与CD相等的线段是DE.
(2)证明小明发现的结论;
参考小明思考问题的方法,解决下面的问题:
(3)如图3,△ABC中,AB=AC,∠BAC=90°,点D在BC上,BD=2DC,点E在AD上,且∠BEC=135°,求$\frac{BE}{CE}$的值.
分析 (1)直接写出答案;
(2)先判断出∠ADC=ADC=∠FEDFED,在判断出FE=AD,即可判断出△FEDFED≌△ADCADC即可;
(3)先判断出∠FBE=FBE=∠GECGEC,进而得出△BFEBFE∽△EGC,得出$\frac{BE}{CE}=\frac{BF}{EG}=\frac{FE}{GC}$,再判断出FE=2EG,即可得出结论.
解答 解:(1)DE;
故答案为:DE;
(2)证明:作EF⊥AB,垂足为F.
则∠BFE=∠DFE=90°═∠A═∠CDE.
∵∠ADC+∠CDE=∠ADE=∠DFE+∠FED,
∴∠ADC=∠FED.
∵∠BFE=90°,∠B=30°,
∴BE=2FE.
∵BE=2AD,
∴FE=AD.
在△FED和△ADC中,$\left\{\begin{array}{l}{∠FED=∠ADC}\\{∠DFE=∠CAD}\\{FE=AD}\end{array}\right.$
∴△FED≌△ADC.
∴DE=CD
(3)如图3,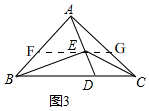
过点E作BC的平行线,与AB、AC分别相交于点F、G.
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°.
∵FG∥BC,
∴∠AFG=∠ABC=∠ACB=∠AGF=45°,∠BFE=135°=∠EGC.
∴AF=AG.BF=GC.
∵∠GEC+∠CEB=∠GEB=∠EFB+∠FBE,
∴∠FBE=∠GEC
∴△BFE∽△EGC.
∴$\frac{BE}{CE}=\frac{BF}{EG}=\frac{FE}{GC}$,
∵FG∥BC,
∴△AFE∽△ABD,△AEG∽△ADC,
∴$\frac{FE}{BD}=\frac{AE}{AD}$,$\frac{AE}{AD}=\frac{EG}{DC}$,
∴$\frac{FE}{BD}=\frac{EG}{DC}$
∵BD=2DC,
∴FE=2EG,
∴$\frac{BF}{EG}=\frac{EF}{CG}=\frac{2EG}{BF}$,
∴$\frac{BF}{EG}=\sqrt{2}$,
∴$\frac{BE}{CE}=\frac{BF}{EG}=\sqrt{2}$
点评 此题是三角形综合题,主要考查了同角的余角相等,全等三角形的判定和性质,相似三角形的判定和性质,解本题的关键是得出FE=2EG,是一道比较简单的中考常考题.

 阅读快车系列答案
阅读快车系列答案| A. | 任何数都不等于它的相反数 | |
| B. | 符号相反的数互为相反数 | |
| C. | 若有理数a,b互为相反数,则它们一定异号 | |
| D. | 若有理数a,b互为相反数,那么a+b=0 |
| A. |  | B. |  | C. |  | D. |  |
| A. | -(-3)=-|-3| | B. | -(2)3=-2×3 | C. | |-$\frac{1}{100}$|>-100 | D. | -24=(-2)4 |
| A. | 30cm | B. | 36cm | C. | 39cm | D. | 33cm |
| A. | 3.98×108 | B. | 398.35×108 | C. | 3.9835×1010 | D. | 3.9835×1011 |
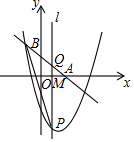 如图,已知直线y=-$\frac{3}{4}$x+1分别交x轴、y轴于点A、B,M是x轴正半轴上一动点,并以每秒1个单位的速度从O点向x轴正方向运动,过点M作x轴的垂线l,与抛物线y=x2-$\frac{5}{2}$x-2交于点P,与直线AB交于点Q,连结BP,经过t秒时,△PBQ是以BQ为腰的等腰三角形,则t的值是2或$\frac{3+\sqrt{21}}{2}$或$\frac{31}{8}$.
如图,已知直线y=-$\frac{3}{4}$x+1分别交x轴、y轴于点A、B,M是x轴正半轴上一动点,并以每秒1个单位的速度从O点向x轴正方向运动,过点M作x轴的垂线l,与抛物线y=x2-$\frac{5}{2}$x-2交于点P,与直线AB交于点Q,连结BP,经过t秒时,△PBQ是以BQ为腰的等腰三角形,则t的值是2或$\frac{3+\sqrt{21}}{2}$或$\frac{31}{8}$.