题目内容
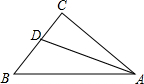 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
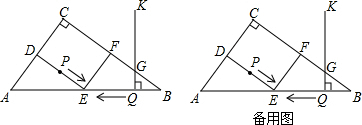
如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.(1)以AB边上一点O为圆心,过A,D两点作⊙O;(用圆规、直尺作图,不写作法,但要保留作图痕迹)
(2)判断直线BC与⊙O的位置关系,并说明理由.
考点:作图—复杂作图,直线与圆的位置关系
专题:
分析:(1)作出AD的垂直平分线交AB于O,再以O为圆心,AO长为半径画圆即可;
(2)连结OD,根据OA=OD,可得∠OAD=∠ODA,再证明OD∥AC,可得∠C=∠BDO=90°,进而得到直线BC与⊙O的位置关系.
(2)连结OD,根据OA=OD,可得∠OAD=∠ODA,再证明OD∥AC,可得∠C=∠BDO=90°,进而得到直线BC与⊙O的位置关系.
解答: 解:(1)如图,⊙O为所求作的圆;
解:(1)如图,⊙O为所求作的圆;
(2)BC与⊙O相切.
连结OD,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠OAD=∠DAC,
∴∠ODA=∠DAC,
∴OD∥AC,
∵∠C=90°,
∴∠BDO=90°,
∴BC与⊙O相切.
 解:(1)如图,⊙O为所求作的圆;
解:(1)如图,⊙O为所求作的圆;(2)BC与⊙O相切.
连结OD,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠OAD=∠DAC,
∴∠ODA=∠DAC,
∴OD∥AC,
∵∠C=90°,
∴∠BDO=90°,
∴BC与⊙O相切.
点评:此题主要考查了直线与圆的位置关系,以及复杂作图,关键是正确画出图形.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
已知果农贩卖的西红柿,其重量与价钱成线型函数关系,今小华向果农买一竹篮的西红柿,含竹篮秤得总重量为15公斤,付西红柿的钱250元.若他再加买0.5公斤的西红柿,需多付10元,则空竹篮的重量为多少公斤?( )
| A、1.5 | B、2 | C、2.5 | D、3 |
若单项式4x2+ay2与
x2a-2y2是同类项,则a为( )
| 1 |
| 3 |
| A、-2 | B、2 | C、3 | D、4 |
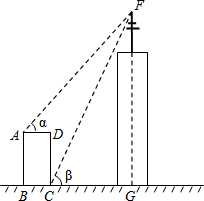 如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点处测得该塔顶端F的仰角分别为∠α=48°,∠β=65°,矩形建筑物宽度AD=20m,高度DC=33m.计算该信号发射塔顶端到地面的高度FG(结果精确到1m).
如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点处测得该塔顶端F的仰角分别为∠α=48°,∠β=65°,矩形建筑物宽度AD=20m,高度DC=33m.计算该信号发射塔顶端到地面的高度FG(结果精确到1m).