题目内容
3.已知|x+y-2|+(x-2y)2=0,则x=$\frac{4}{3}$、y=$\frac{2}{3}$.分析 利用非负数的性质列出方程组,求出方程组的解即可得到x与y的值.
解答 解:∵|x+y-2|+(x-2y)2=0,
∴$\left\{\begin{array}{l}{x+y=2}\\{x-2y=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{4}{3}}\\{y=\frac{2}{3}}\end{array}\right.$.
故答案为:$\frac{4}{3}$;$\frac{2}{3}$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法为:加减消元法与代入消元法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.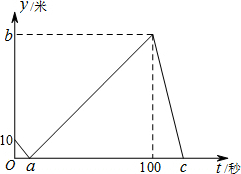 甲乙两人在直线跑道上同起点、同终点、同方向匀速跑步600米,先到终点的人原地休息,已知甲先出发2秒.在跑步过程中,甲乙两人间的距离y(米)与乙出发的时间t(秒)的关系如图所示.给出下列结论:①a=8,②b=90,③c=120,其中正确的是( )
甲乙两人在直线跑道上同起点、同终点、同方向匀速跑步600米,先到终点的人原地休息,已知甲先出发2秒.在跑步过程中,甲乙两人间的距离y(米)与乙出发的时间t(秒)的关系如图所示.给出下列结论:①a=8,②b=90,③c=120,其中正确的是( )
 甲乙两人在直线跑道上同起点、同终点、同方向匀速跑步600米,先到终点的人原地休息,已知甲先出发2秒.在跑步过程中,甲乙两人间的距离y(米)与乙出发的时间t(秒)的关系如图所示.给出下列结论:①a=8,②b=90,③c=120,其中正确的是( )
甲乙两人在直线跑道上同起点、同终点、同方向匀速跑步600米,先到终点的人原地休息,已知甲先出发2秒.在跑步过程中,甲乙两人间的距离y(米)与乙出发的时间t(秒)的关系如图所示.给出下列结论:①a=8,②b=90,③c=120,其中正确的是( )| A. | 仅有①② | B. | 仅有② | C. | 仅有②③ | D. | ①②③ |
11.若关于x的不等式mx-n>0的解集是x<$\frac{1}{4}$,则关于x的不等式(n-m)x>(m+n)的解集是( )
| A. | x<-$\frac{5}{3}$ | B. | x>-$\frac{5}{3}$ | C. | x<$\frac{5}{3}$ | D. | x>$\frac{5}{3}$ |
18.在一次野炊活动中,小明所在的班级有x人,分成y组,若每组7人,则余下3人;若每组8人,则缺5人,求全班人数的正确的方程组是( )
| A. | $\left\{\begin{array}{l}{7y=x-3}\\{8y=x+5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{7y=x+3}\\{8y=x-5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{7x=y+3}\\{8x=y-5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{7x=y-3}\\{8x=y+5}\end{array}\right.$ |
12.如图所示的是某几何体的三视图及相关数据,则该几何体的侧面积是( )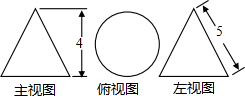

| A. | 30π | B. | 24π | C. | 15π | D. | 12π |
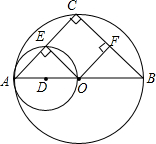 如图,AB是⊙O的直径,AC是⊙O的弦,以OA为直径的⊙D与AC相交于点E.
如图,AB是⊙O的直径,AC是⊙O的弦,以OA为直径的⊙D与AC相交于点E.