题目内容
13.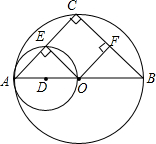 如图,AB是⊙O的直径,AC是⊙O的弦,以OA为直径的⊙D与AC相交于点E.
如图,AB是⊙O的直径,AC是⊙O的弦,以OA为直径的⊙D与AC相交于点E.(1)试判断线段OE与线段BC的关系,并说明理由;
(2)若F为BC边上的中点,试判定四边形OFCE的形状.
分析 (1)先由圆周角定理得出∠ACB=AEO=90°得出OE∥BC,再由点O是AB的中点可知,OE是△ABC的中位线,由三角形的中位线定理即可得出结论;
(2)由点O是AB的中点,F为BC边上的中点可知,OF是△ABC的中位线,由三角形的中位线定理得出OF∥AC,从而得出∠OFC=∠ACB=90°,即可证得四边形OFCE是矩形.
解答 解:(1)OE∥BC,OE=$\frac{1}{2}$BC;
∵AB是⊙O的直径,AO是⊙D的直径,
∴∠ACB=AEO=90°,
∴OD∥BC,
∵点O是AB的中点,
∴OE是△ABC的中位线,
∴OE∥BC,OE=$\frac{1}{2}$BC;
(2)四边形OFCE是矩形;
∵点O是AB的中点,F为BC边上的中点,
∴OF∥AC,
∴∠OFC=∠ACB=90°,
∵∠ACB=AEO=90°,
∴四边形OFCE是矩形.
点评 本题考查了圆周角定理、三角形中位线定理、矩形的判定等,熟练掌握圆周角定理、三角形中位线定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.$\sqrt{({-2015)}^{2}}$=( )
| A. | -2015 | B. | 2015 | C. | ±2015 | D. | $\frac{1}{2015}$ |
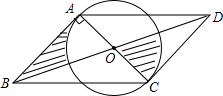 如图,平行四边形ABCD中,AB=AC=4,AB⊥AC,O是对角线的交点,若⊙O过A、C两点,则图中阴影部分的面积之和为4.
如图,平行四边形ABCD中,AB=AC=4,AB⊥AC,O是对角线的交点,若⊙O过A、C两点,则图中阴影部分的面积之和为4.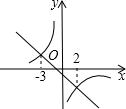 定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.如max{-3,2}=2.
定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.如max{-3,2}=2.