题目内容
12.计算(1)2$\sqrt{8}$+6$\sqrt{\frac{1}{2}}$-3$\sqrt{32}$
(2)2sin45°-$\frac{1}{\sqrt{2}+1}$+sin235°+cos235°.
分析 根据二次根式的混合运算法则、特殊角的三角函数值计算即可.
解答 解:(1)2$\sqrt{8}$+6$\sqrt{\frac{1}{2}}$-3$\sqrt{32}$
=4$\sqrt{2}$+3$\sqrt{2}$-12$\sqrt{2}$
=-5$\sqrt{2}$;
(2)2sin45°-$\frac{1}{\sqrt{2}+1}$+sin235°+cos235°
=2×$\frac{\sqrt{2}}{2}$-($\sqrt{2}$-1)+1
=$\sqrt{2}$-$\sqrt{2}$+1+1
=2.
点评 本题考查的是实数的运算,掌握二次根式的混合运算法则、特殊角的三角函数值是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
13.如果A(2,y1),B(3,y2)两点都在反比例函数y=$\frac{1}{x}$的图象上,那么y1与y2的大小关系是( )
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | y1≥y2 |
20.从二次根式$\sqrt{12}$、$\sqrt{{x}^{2}+3}$、$\sqrt{\frac{3}{2}}$、$\sqrt{{a}^{2}b}$、2$\sqrt{0.5}$、$\sqrt{26}$中任选一个,不是最简二次根式的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
7.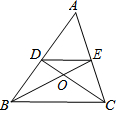 如图,△ABC的两条中线BE、CD交于O,则S△EDO:S△ADE=( )
如图,△ABC的两条中线BE、CD交于O,则S△EDO:S△ADE=( )
 如图,△ABC的两条中线BE、CD交于O,则S△EDO:S△ADE=( )
如图,△ABC的两条中线BE、CD交于O,则S△EDO:S△ADE=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:6 |
4.43表示的意义是( )
| A. | 4×3 | B. | 4个3相加 | C. | 4个3相乘 | D. | 3个4相乘 |
2.若单项式-2am+2b与5ab2m+n是同类项,则mn的值是( )
| A. | 1 | B. | -1 | C. | 16 | D. | -32 |
 如图,已知在△ABC中,∠1=∠2,∠3=∠4,∠BAC=84°.求∠DAC的度数.
如图,已知在△ABC中,∠1=∠2,∠3=∠4,∠BAC=84°.求∠DAC的度数.