题目内容
20.若数轴上的任意一点P表示的数是x,且|x-a|+|x-b|的最小值为4,若a=3,则b的值为7或-1.分析 根据线段上的点到线段两端点的距离的和最小,分类讨论可得答案.
解答 解:由线段上的点到线段两端点的距离的和最小,
①当点b在a的右侧时,
得P在3点与b点的线段上,|x-3|+|x-b|的值最小为4,
|x-3|+|x-b|最小=x-3+b-x=4,
解得:b=7;
②当点b在a的左侧时,
得P在3点与b点的线段上,|x-3|+|x-b|的值最小为4,
|x-3|+|x-b|最小=3-x+x-b=4,
解得:b=-1;
故答案为:7或-1,.
点评 本题考查了绝对值,利用线段上的点到线段两端点的距离的和最小是解答此题的关键.

练习册系列答案
相关题目
6.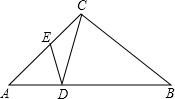 如图,AC=BC=BD,AD=AE,DE=CE,则∠B为( )度.
如图,AC=BC=BD,AD=AE,DE=CE,则∠B为( )度.
 如图,AC=BC=BD,AD=AE,DE=CE,则∠B为( )度.
如图,AC=BC=BD,AD=AE,DE=CE,则∠B为( )度.| A. | 30° | B. | 36° | C. | 40° | D. | 45° |
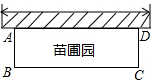 某苗圃场准备围建一个矩形新品种苗圃要求四周要围好,其中一边靠墙,另外三边用周长是32米的篱笆围成
某苗圃场准备围建一个矩形新品种苗圃要求四周要围好,其中一边靠墙,另外三边用周长是32米的篱笆围成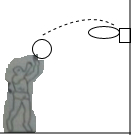 一位运动员在距篮下4m处起跳投篮,恰好投中,球出手时离地面高度为2.25m,球运行的路线是抛物线,已知篮筐中心离地面的距离是3.05m,当球运行的水平距离是2.5m时,球达到最大高度,问球达到最大高度时距离地面多少米?
一位运动员在距篮下4m处起跳投篮,恰好投中,球出手时离地面高度为2.25m,球运行的路线是抛物线,已知篮筐中心离地面的距离是3.05m,当球运行的水平距离是2.5m时,球达到最大高度,问球达到最大高度时距离地面多少米?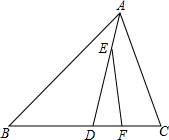 如图,在△ABC中,AD平分∠BAC且与BC相交于点D,∠B=40°,∠BAD=30°.
如图,在△ABC中,AD平分∠BAC且与BC相交于点D,∠B=40°,∠BAD=30°.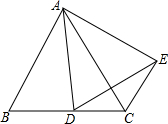 如图,△ABC是等边三角形,AD=AE,BD=CE,求∠ACE的度数.
如图,△ABC是等边三角形,AD=AE,BD=CE,求∠ACE的度数.