题目内容
10．
甲、乙两名同学在一次用频率去估计概率的实验中，统一了某一结果出现的频率绘出的统计图如图所示，则符合这一结果的实验可能是（ ）| A． | 从一个装有2个白球和1个红球的袋子中任取两球，取到两个白球的概率 | |
| B． | 任意写一个正整数，它能被2整除的概率 | |
| C． | 抛一枚硬币，连续两次出现正面的概率 | |
| D． | 掷一枚正六面体的骰子，出现1点的概率 |
分析 根据统计图可知，试验结果在0.33附近波动，即其概率P≈0.33，计算四个选项的概率，约为0.33者即为正确答案．
解答 解：A、画树形图得：
所以从一个装有2个白球和1个红球的袋子中任取两球，取到两个白球的概率$\frac{1}{3}$；故此选项正确；
B、任意写一个整数，它能2被整除的概率为$\frac{1}{2}$；故此选项错误；
C、列表如下：
| 正 | 反 | |
| 正 | （正，正） | （反，正） |
| 反 | （正，反） | （反，反） |
D、掷一枚正六面体的骰子，出现1点的概率为$\frac{1}{6}$，故此选项错误；
故选：A．
点评 此题考查了利用频率估计概率，大量反复试验下频率稳定值即概率．用到的知识点为：频率=所求情况数与总情况数之比．同时此题在解答中要用到概率公式
练习册系列答案
金钥匙试卷系列答案
相关题目
如图，∠C=∠1，∠2与∠D互余，BE⊥DF，垂足为G．求证：AB∥CD．
1．下列等式正确的是（ ）
| A． | -|3|=|-3| | B． | |3|=|-3| | C． | |-3|=-3 | D． | -（-3）=-|-3| |
如图，直线y=$\frac{1}{2}$x+1与x轴、y轴分别相交于点A、B，二次函数的图象与y轴相交于点C，与直线y=$\frac{1}{2}$x+1相交于点A、D，CD∥x轴，∠CDA=∠OCA．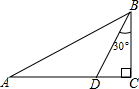
如图所示，在△ABC中，∠C=90°，AB=4$\sqrt{3}$．点D在边AC上，且AD=BD，∠DBC=30°．求：
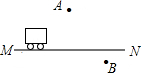如图所示，一辆汽车在平直的公路上由M向N方向行驶，A、B分别是位于公路MN两侧的村庄．
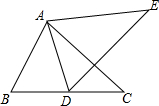如图，AB=AD，∠BAD=∠EAC，∠C=∠E，求证：AE=AC．
4．平面直角坐标系中，O为坐标原点，点A的坐标为（$\sqrt{3}$，1），将OA绕原点按逆时针方向旋转90°得OB，则点B的坐标为（ ）
| A． | （1，$\sqrt{3}$） | B． | （-1，$\sqrt{3}$） | C． | （0，2） | D． | （2，0） |