题目内容
15. 已知,如图,点D,E,F分别在△ABC的边AB,AC,BC上,且DE∥BC,EF∥AB,求证:$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{BF}{BC}$=$\frac{DE}{BC}$.
已知,如图,点D,E,F分别在△ABC的边AB,AC,BC上,且DE∥BC,EF∥AB,求证:$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{BF}{BC}$=$\frac{DE}{BC}$.
分析 由△ADE∽△ABC,可得$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{DE}{BC}$,由EF∥AB,可得$\frac{AE}{AC}$=$\frac{BF}{BC}$,由此即可证明.
解答 证明: ∵DE∥BC,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{DE}{BC}$,
∵EF∥AB,
∴$\frac{AE}{AC}$=$\frac{BF}{BC}$,
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{BF}{BC}$=$\frac{DE}{BC}$.
点评 本题考查相似三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是熟练掌握这些知识,属于基础题,中考常考题型.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
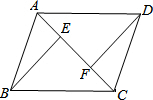 如图,AB=CD,BE⊥AC于点E,DF⊥AC于点F,AF=CE,求证:△ABE≌△CDF.
如图,AB=CD,BE⊥AC于点E,DF⊥AC于点F,AF=CE,求证:△ABE≌△CDF.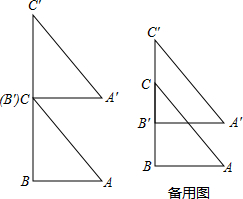 如图,已知:Rt△ABC中,∠B=90°,AB=6,BC=8,△A′B′C′≌△ABC,BC与B′C′在同一直线上,点C与点B′重合(如图1),现将△ABC沿射线B′C′以2个单位/秒的速度向上平移,设运动时间为t(s).
如图,已知:Rt△ABC中,∠B=90°,AB=6,BC=8,△A′B′C′≌△ABC,BC与B′C′在同一直线上,点C与点B′重合(如图1),现将△ABC沿射线B′C′以2个单位/秒的速度向上平移,设运动时间为t(s).