Question

15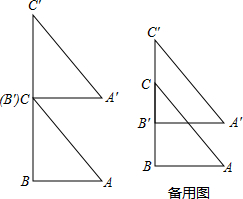．如图，已知：Rt△ABC中，∠B=90°，AB=6，BC=8，△A′B′C′≌△ABC，BC与B′C′在同一直线上，点C与点B′重合（如图1），现将△ABC沿射线B′C′以2个单位/秒的速度向上平移，设运动时间为t（s）．
（1）当0＜t＜4时，设AC与A′B′交于点D，求B′C•A′D的最大值；
（2）求当t为何值时，△A′B′C′与△ABC重叠部分的面积是18．

Answer 1

分析 （1）根据同角的三角函数表示出B′D、A′D，计算它们的积，并根据二次函数的顶点坐标求最值；
（2）重叠部分是三角形，根据（1）的值利用面积公式计算．

解答 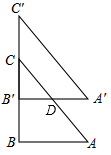解：（1）由题意得：B′C=2t，
则tan∠A=$\frac{BC}{AB}=\frac{B′C}{B′D}$，
∴$\frac{8}{6}=\frac{2t}{B′D}$，
∴B′D=$\frac{12t}{8}$=$\frac{3t}{2}$，
∴A′D=6-$\frac{3}{2}t$，
∴B′C•A′D=2t•（6-$\frac{3}{2}t$）=-3t²+12t=-3（t-2）²+12，
∵-3＜0，
∴B′C•A′D有最大值，
当t=2时，B′C•A′D最大值为12；
（2）S_重叠部分=S_△CB′D=$\frac{1}{2}$B′C•B′D=$\frac{1}{2}$×2t×$\frac{3}{2}$t=18，
t²=12，
t=±2$\sqrt{3}$，
∵0＜t＜4，
∴t=2$\sqrt{3}$，
则当t为2$\sqrt{3}$时，△A′B′C′与△ABC重叠部分的面积是18．

点评 本题是三角形与二次函数的综合问题，考查了动点问题中的路程、速度与时间的关系；本题把两条线段的乘积的最值问题转化为二次函数的最值问题，很容易就能求出结论．