题目内容
12. △ABC中,AB=AC,以AC为直径作⊙O交BC于D,过D作⊙O的切线DE交AB于E,求证:
△ABC中,AB=AC,以AC为直径作⊙O交BC于D,过D作⊙O的切线DE交AB于E,求证:(1)DE⊥AB
(2)CD2=EB•AB.
分析 (1)连接OD.由等腰三角形的性质得出∴∠B=∠ODC,求出OD∥AB,再由切线的性质得出DE⊥AB,即可得出结论;
(2)连接AD,由等腰三角形的性质得出BD=CD,证明△BDE∽△BAD,得出对应边成比例,即可得出结论.
解答 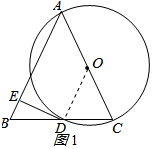 证明:(1)连接OD,如图1所示:
证明:(1)连接OD,如图1所示:
∵AB=AC,OD=OC,
∴∠B=∠C,∠ODC=∠C,
∴∠B=∠ODC,
∴OD∥AB,
∵DE是⊙O的切线,
∴OD⊥DE,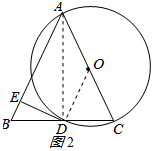
∴DE⊥AB;
(2)连接AD,如图2所示:
∵AC为⊙O的直径,
∴∠ADB=∠ADC=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
∵DE⊥AB,
∴∠DEB=90°=∠ADB,
又∵∠B=∠B,
∴△BDE∽△BAD,
∴BD:AB=EB:BD,
∴BD2=EB•AB,
∴CD2=EB•AB.
点评 本题主要考查的是圆周角定理、切线的性质、等腰三角形的性质和判定、三角形的内角和定理,掌握此类问题的辅助线的作法是解题的关键.

练习册系列答案
相关题目
 一座隧道的截面由抛物线和长方形组成,长方形的长为8m,宽为2m,隧道的最高点P位于AB的中央且距地面6m,建立如图所示的坐标系.
一座隧道的截面由抛物线和长方形组成,长方形的长为8m,宽为2m,隧道的最高点P位于AB的中央且距地面6m,建立如图所示的坐标系.
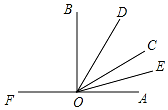 如图,点O是直线FA上一点,OB,OD,OC,OE是射线,OE平分∠AOC,OD平分∠BOC.
如图,点O是直线FA上一点,OB,OD,OC,OE是射线,OE平分∠AOC,OD平分∠BOC. 如图,已知BE⊥AD,CF⊥AD,且BE=CF.请你判断AD是△ABC的中线还是角平分线?请说明你的理由.
如图,已知BE⊥AD,CF⊥AD,且BE=CF.请你判断AD是△ABC的中线还是角平分线?请说明你的理由. 如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.
如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.