题目内容
4．
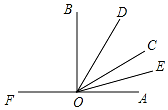如图，点O是直线FA上一点，OB，OD，OC，OE是射线，OE平分∠AOC，OD平分∠BOC．（1）若∠AOE=20°，求∠FOC的度数；
（2）若∠AOB=88°，求∠DOE的度数．
分析 （1）可求∠AOC的度数，然后利用邻补角的性质即可求出∠FOC的度数．
（2）根据OE平分∠AOC，OD平分∠BOC可知：∠DOE=$\frac{1}{2}$（∠BOC+∠AOC）=$\frac{1}{2}$∠AOB．
解答 解：（1）∵OE平分∠AOC
∴∠AOC=2∠AOE=40°，
∴∠FOC=180°-∠AOC=140°
（2）∵OE平分∠AOC，OD平分∠BOC，
∴∠COD=$\frac{1}{2}$∠BOC，∠COE=$\frac{1}{2}$∠AOC，
∴∠DOE=$\frac{1}{2}$（∠BOC+∠AOC）=$\frac{1}{2}$∠AOB=44°
点评 本题考查角的计算，涉及角平分线的性质，属于基础题型．
练习册系列答案
ABC考王全优卷系列答案
相关题目
在△ABC中，∠ACB=90°，O为边AB上的一点，以O为圆心，以OA为半径，作⊙O，交AB于点D，交AC于点E，交BC于点F，且点F恰好是ED的中点，连接DF．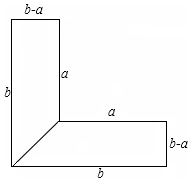
李红的叔叔在郊区种菜，他家有一块L形菜地，要把L形菜地按如图所示的那样分成面积相等的两个梯形，种上不同的蔬菜．这两个梯形的上底都是a米，下底都是b米，高都是（b-a）米．
△ABC中，AB=AC，以AC为直径作⊙O交BC于D，过D作⊙O的切线DE交AB于E，求证：