题目内容
1．
如图，已知BE⊥AD，CF⊥AD，且BE=CF．请你判断AD是△ABC的中线还是角平分线？请说明你的理由．
分析 证明△BDE和△CDF全等来确定其为中线．
解答 解：AD是△ABC的中线．理由如下：
∵BE⊥AD，CF⊥AD，
∴∠BED=∠CFD=90°，
在△BDE和△CDF中，$\left\{\begin{array}{l}{∠BED=∠CFD}&{\;}\\{∠BDE=∠CDF}&{\;}\\{BE=CF}&{\;}\end{array}\right.$，
∴△BDE≌△CDF（AAS），
∴BD=CD．
∴AD是△ABC的中线．
点评 本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
练习册系列答案
阅读快车系列答案
相关题目
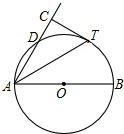如图，AB是⊙O直径，D为⊙O上一点，AT平分∠BAD交⊙O于点T，过T作AD的垂线交AD的延长线于点C．
△ABC中，AB=AC，以AC为直径作⊙O交BC于D，过D作⊙O的切线DE交AB于E，求证：
已知抛物线y=-x2+bx+c与x轴交于点A（m-2，0）和B（2m+1，0）（点A在点B的左侧），与y轴相交于点C，对称轴为l：x=1．