题目内容
7.一只不透明的布袋里装有4个大小、质地均相同的乒乓球,每个球上面分别标有1、2、3、4.小林先从布袋中随机抽取一个乒乓球(不放回),再从剩下的3个球中随机抽取第二个乒乓球.记两次取得乒乓球上的数字依次为a、b(1)求a、b之积为奇数的概率.
(2)若c=5,求长为a、b、c的三条线段能围成三角形的概率.
分析 (1)画树状图展示所有12种等可能的结果数,再找出a、b之积为奇数的结果数,然后根据概率公式求解;
(2)根据三角形三边的关系,找出长为a、b、c的三条线段能围成三角形的结果数,然后根据概率公式求解.
解答 解:(1)画树状图:
共有12种等可能的结果数,其中a、b之积为奇数的结果数为2,
所以a、b之积为奇数的概率=$\frac{2}{12}$=$\frac{1}{6}$;
(2)长为a、b、c的三条线段能围成三角形的结果数为4,
所以长为a、b、c的三条线段能围成三角形的概率=$\frac{4}{12}$=$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.

练习册系列答案
相关题目
17.为增强公民节水意识,合理利用水资源,某市采用“阶梯收费”,标准如下表:
譬如:某用户2月份用水9m3,则应缴水费:2×6+4×(9-6)=24(元)
(1)某用户3月用水15m3应缴水费多少元?
(2)已知某用户4月份缴水费20元,求该用户4月份的用水量;
(3)如果该用户5、6月份共用水20m3 (6月份用水量超过5月份用水量),共交水费64元,则该户居民5、6月份各用水多少立方米?
| 用水量 | 单价 |
| 不超过6m3的部分 | 2元/m3 |
| 超过6m3不超过10m3的部分 | 4元/m3 |
| 超出10m3的部分 | 8元/m3 |
(1)某用户3月用水15m3应缴水费多少元?
(2)已知某用户4月份缴水费20元,求该用户4月份的用水量;
(3)如果该用户5、6月份共用水20m3 (6月份用水量超过5月份用水量),共交水费64元,则该户居民5、6月份各用水多少立方米?
 如图,△ABC在方格纸中,设单元格边长为1.
如图,△ABC在方格纸中,设单元格边长为1.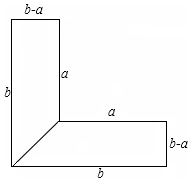 李红的叔叔在郊区种菜,他家有一块L形菜地,要把L形菜地按如图所示的那样分成面积相等的两个梯形,种上不同的蔬菜.这两个梯形的上底都是a米,下底都是b米,高都是(b-a)米.
李红的叔叔在郊区种菜,他家有一块L形菜地,要把L形菜地按如图所示的那样分成面积相等的两个梯形,种上不同的蔬菜.这两个梯形的上底都是a米,下底都是b米,高都是(b-a)米. △ABC中,AB=AC,以AC为直径作⊙O交BC于D,过D作⊙O的切线DE交AB于E,求证:
△ABC中,AB=AC,以AC为直径作⊙O交BC于D,过D作⊙O的切线DE交AB于E,求证: