题目内容
3.已知:m、n是方程x2+2x-5=0的两个实数根,则m2-mn+2m=10.分析 由根与系数的关系可找出“m+n=-$\frac{b}{a}$=-2,mn=$\frac{c}{a}$=-5”,在算式m2-mn+2m中,提取m得到m(m-n+2),将2换成-(m+n),再进行计算即可得出结论.
解答 解:∵m、n是方程x2+2x-5=0的两个实数根,
∴m+n=-$\frac{b}{a}$=-2,mn=$\frac{c}{a}$=-5.
∵m2-mn+2m=m(m-n+2)=m[(m-n)-(m+n)]=-2mn=-2×(-5)=10.
故答案为:10.
点评 本题考查了根与系数的关系,解题的关键是将将2换成-(m+n).本题属于基础题,难度不大,解决该题型题目时,利用根与系数的关系得出两根之和与两根之积是关键.

练习册系列答案
相关题目
13.下列计算正确的是( )
| A. | a2+a2=a4 | B. | 2a-a=2 | C. | (a2)3=a5 | D. | (ab)2=a2b2 |
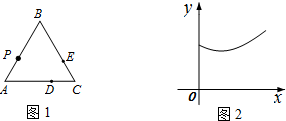
 如图,把△ABC绕点C顺时针旋转40°,得到△A1B1C,边A1B1交AC于点D,∠B1DC=100°,则∠A的度数为60°.
如图,把△ABC绕点C顺时针旋转40°,得到△A1B1C,边A1B1交AC于点D,∠B1DC=100°,则∠A的度数为60°.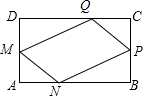 在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化.如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=xcm,已知矩形的边BC=200m,边AB=am,a为大于200的常数,设四边形MNPQ的面积为sm2
在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化.如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=xcm,已知矩形的边BC=200m,边AB=am,a为大于200的常数,设四边形MNPQ的面积为sm2