题目内容
 如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=8cm,求点B到地面的距离.
如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=8cm,求点B到地面的距离.考点:勾股定理的应用
专题:
分析:在Rt△ADE中,运用勾股定理可求出梯子的总长度,在Rt△ABC中,根据已知条件再次运用勾股定理可求出BC的长.
解答:解:在Rt△DAE中,
∵∠DAE=45°,
∴∠ADE=∠DAE=45°
AE=DE=8,
∴AD2=AE2+DE2=82+82=128
∴AD=8
,即梯子的总长为8
米.
∴AB=AD=8
在Rt△ABC中,
∵∠BAC=60°,
∴∠ABC=30°;
∴AC=
AB=4
;
∴BC2=AB2-AC2=(8
)2-(4
)2=96;
∴BC=
=4
m;
∴点B到地面的垂直距离BC=4
m.
∵∠DAE=45°,
∴∠ADE=∠DAE=45°
AE=DE=8,
∴AD2=AE2+DE2=82+82=128
∴AD=8
| 2 |
| 2 |
∴AB=AD=8
| 2 |
在Rt△ABC中,
∵∠BAC=60°,
∴∠ABC=30°;
∴AC=
| 1 |
| 2 |
| 2 |
∴BC2=AB2-AC2=(8
| 2 |
| 2 |
∴BC=
| 96 |
| 6 |
∴点B到地面的垂直距离BC=4
| 6 |
点评:本题考查了勾股定理的应用,如何从实际问题中整理出直角三角形并正确运用勾股定理是解决此类题目的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
一筐苹果4千克,增加
后,列出的算式为( )
| 1 |
| 2 |
A、4+
| ||
B、4×(1+
| ||
| C、4÷(1+) | ||
D、4×(1-
|
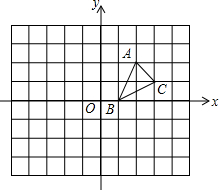 如图,在建立了平面直角坐标系的正方形网格中,A(2,2),B(1,0),C(3,1)
如图,在建立了平面直角坐标系的正方形网格中,A(2,2),B(1,0),C(3,1)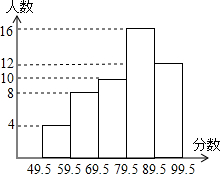 对某班学生一次数学测试成绩进行统计分析,各分数段的人数如图(分数取正整数),请观察图形,并回答下列问题:
对某班学生一次数学测试成绩进行统计分析,各分数段的人数如图(分数取正整数),请观察图形,并回答下列问题: 如图,∠1=∠2,∠3=∠4,∠A=80°,求∠BOC的度数.
如图,∠1=∠2,∠3=∠4,∠A=80°,求∠BOC的度数.