题目内容
16.已知等边三角形的边长为a,则它边上的高、面积分别是( )| A. | $\frac{a}{2}$,$\frac{{a}^{2}}{4}$ | B. | $\frac{\sqrt{3}a}{2}$,$\frac{{a}^{2}}{4}$ | C. | $\frac{\sqrt{3}a}{2}$,$\frac{\sqrt{3}{a}^{2}}{4}$ | D. | $\frac{3a}{4}$,$\frac{\sqrt{3}{a}^{2}}{4}$ |
分析 作出等边三角形一边上的高,利用60°的正弦值可得三角形一边上的高,乘以边长除以2即为等边三角形的面积.
解答  解:如图作AD⊥BC于点D.
解:如图作AD⊥BC于点D.
∵△ABC为等边三角形,
∴∠B=60°,
∴AD=AB×sin∠B=$\frac{\sqrt{3}}{2}$a,
∴边长为a的等边三角形的面积为$\frac{1}{2}$×a×$\frac{\sqrt{3}}{2}$a=$\frac{\sqrt{3}}{4}$a2,
故选C.
点评 本题考查了等边三角形的性质,三角形的面积的求法;利用60°的正弦值得到等边三角形一边上的高是解决本题的突破点.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
7.已知a、b互为相反数,且a-2b=3,则a的值是( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
11.一元二次方程x2-4x+4=0的根的情况为( )
| A. | 只有一个实数根 | B. | 有两个不相等的实数根 | ||
| C. | 有两个相等的实数根 | D. | 没有实数根 |
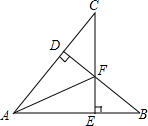 已知,如图,CE⊥AB,BD⊥AC,∠B=∠C,BF=CF.求证:AF为∠BAC的平分线.
已知,如图,CE⊥AB,BD⊥AC,∠B=∠C,BF=CF.求证:AF为∠BAC的平分线.